02. RDBMS

Last updated - 2023년 04월 24일 Edit Source

유튜버 쉬운코드 님의 데이터베이스 강의를 정리한 내용

• relation이라는 개념 자체가, 수학에서 나온 개념이라서 그것부터 보겠다.

set

• 서로 다른 요소(elements)를 가지는 collection
  • 즉, 중복된 요소를 가지고 있지 않다.
• 하나의 set에서 elements의 순서는 중요하지 않다.
  • ex) {1, 3, 11, 4, 7}

relation in mathematics

• 카테시안 곱의 부분집합
• 튜플들의 집합

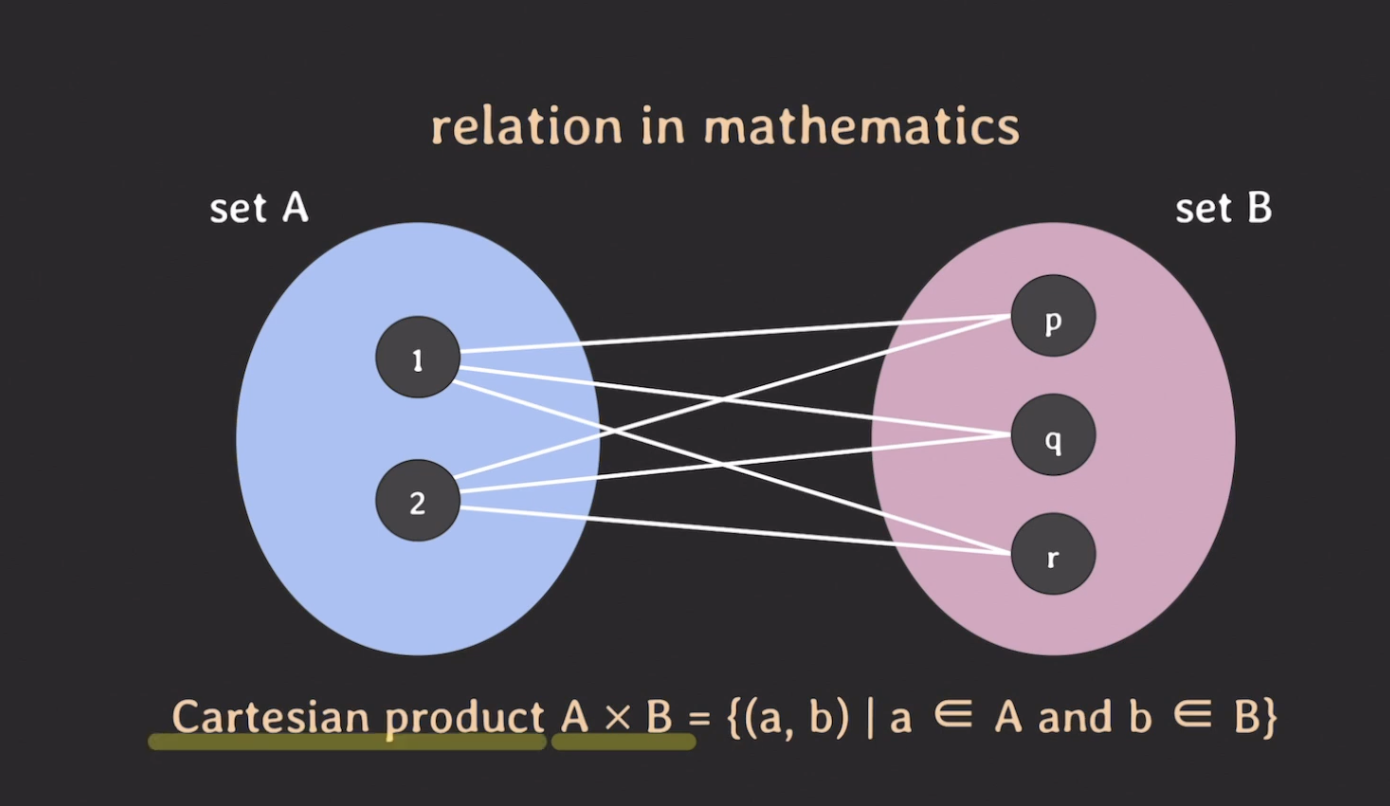
• set A에서 요소를 하나 고르고, set B에서 요소를 하나 골라서 두 개의 요소로 쌍(pair)을 만들어보자.
• 이렇게 가능한 모든 쌍(pair)을 수학에서는 A X B와 같이 나타낼 수 있음
• 이렇게 표현하는 것을 카테시안 곱(Cartesian product)라고 한다.
  • 집합 A에서 a를 하나 고르고, 집합 B에서 b를 하나 골라서 가능한 모든 쌍(pair)

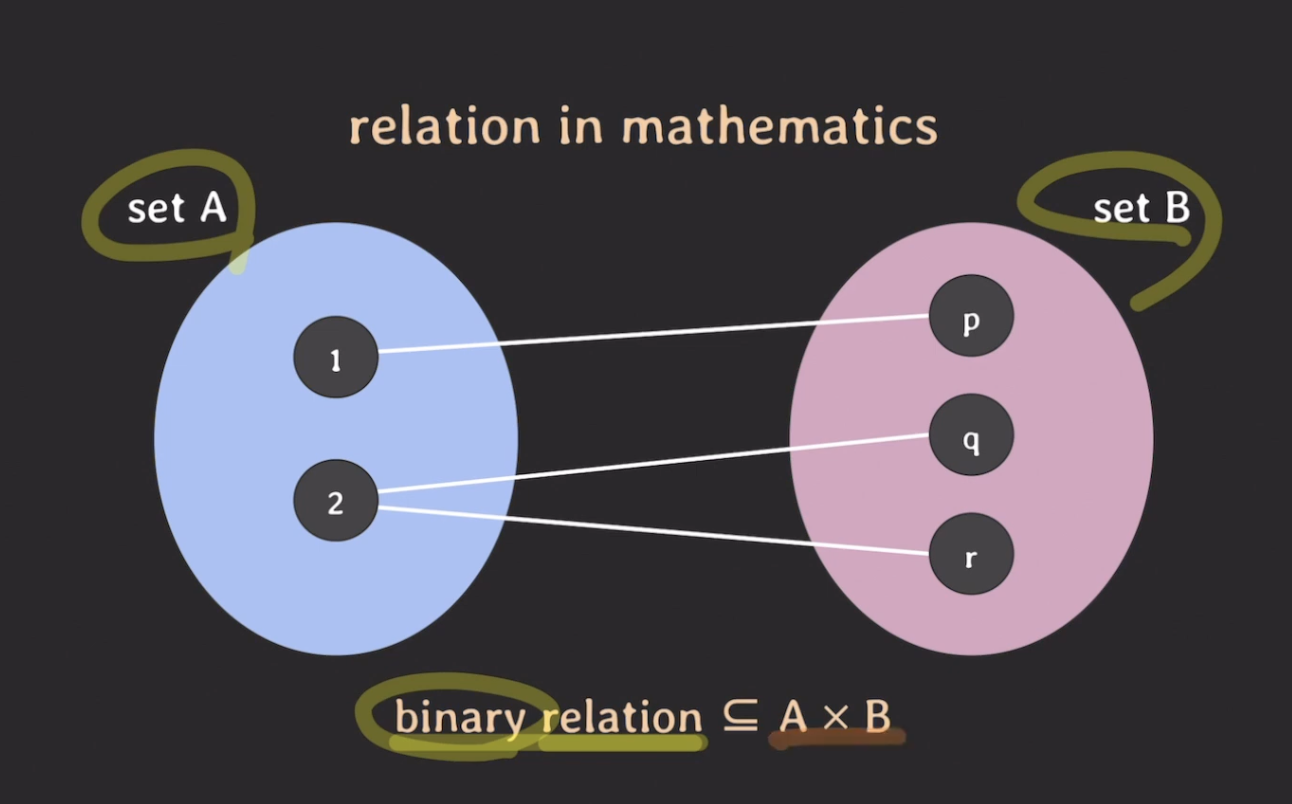
• set이 2개 밖에 없는 경우 binary relation이라고 한다.
• A와 B의 카테시안 곱의 부분집합을 의미

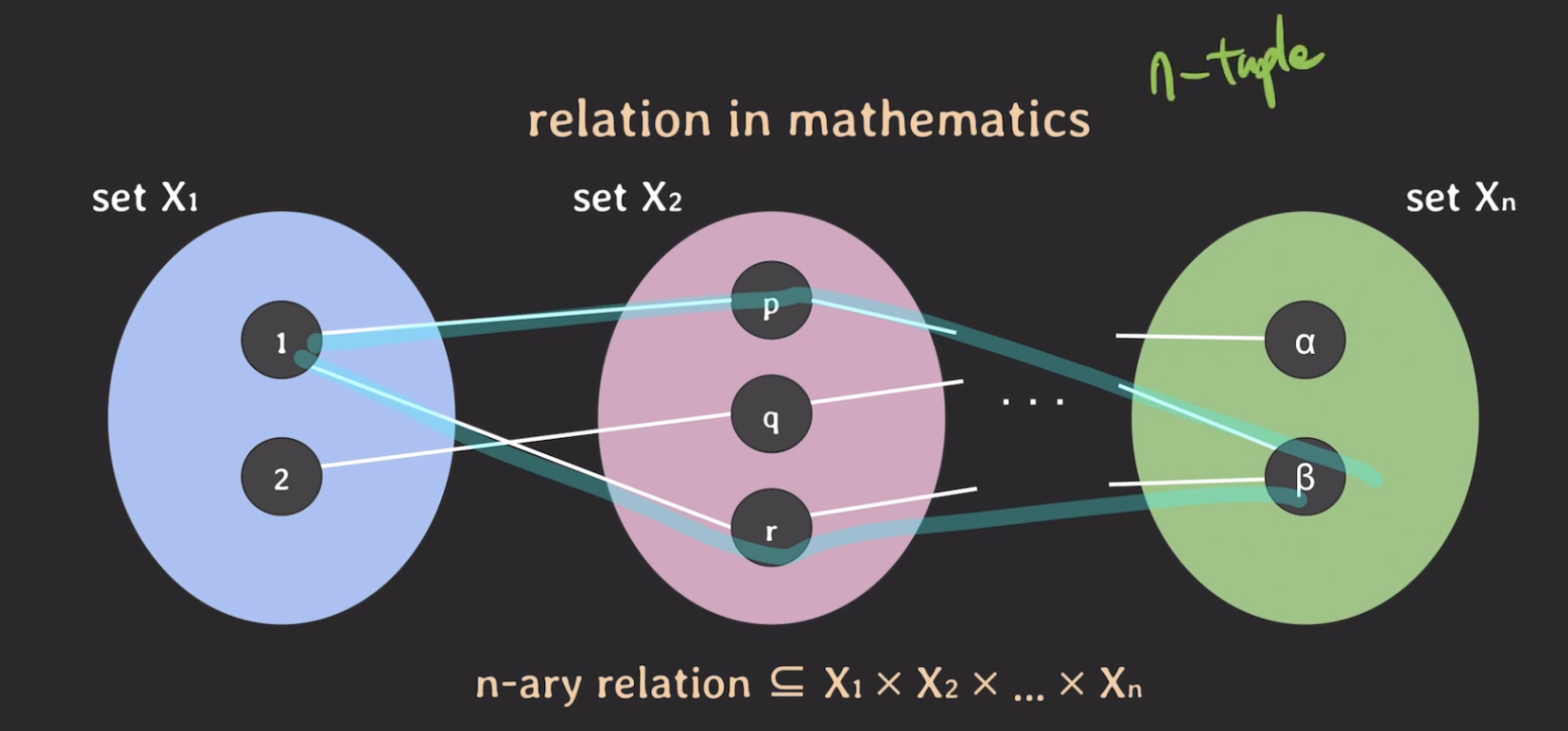
• 총 n개의 set이 있다고 하자.
• 위에서는 집합이 2개라서 binary relation이었지만, 지금은 n개니까 n-ary relation이라고 한다.
• n개의 집합에 대한 카테시안 곱의 부분집합을 의미
• 이때 [1, p, a]와 같이 각각의 리스트를 튜플(Tuple) 이라고 부를 수 있음
• 몇 개의 element 들로 이루어진 리스트라는 의미
• n개의 집합에 대한 튜플이기 때문이 이런 경우에 n-튜플이라고 함

수학에서의 relation이 어떤 의미인지는 봤고, 관계형 데이터 모델(relational data model) 에서 이 개념이 어떻게 적용될까? => 데이터 모델 복습은 1강에서

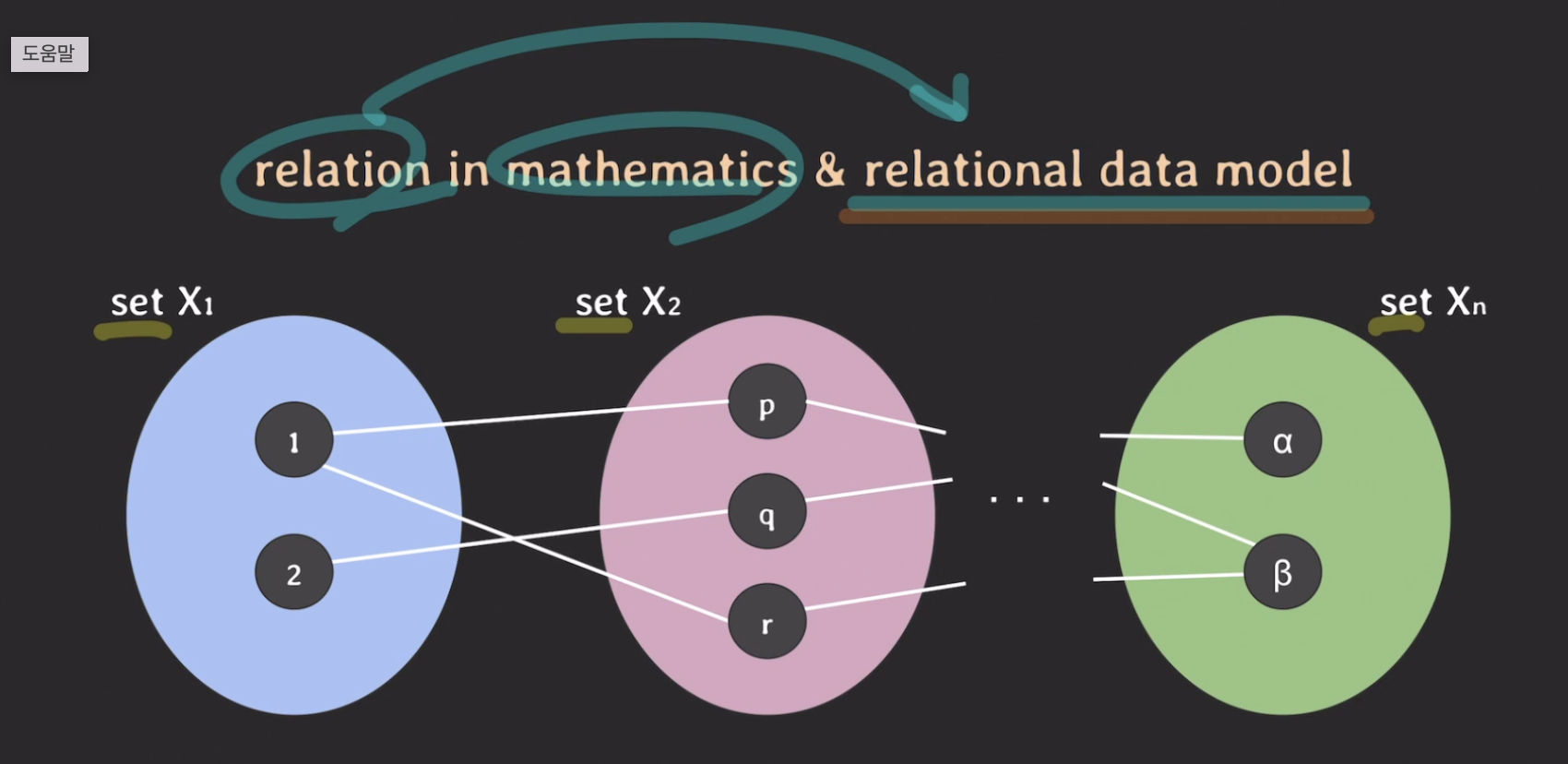
• relational data model에서 set은 domain을 의미
• element 혹은 value 들의 집합이 domain!

이제부터, 학생 데이터를 저장하는 student를 어떻게 relational data model에서 relation으로 표현하는지 살펴보자.

도메인 (domain) : 더이상 나눌 수 없는 값들로 이루어진 집합

domain 정의하기

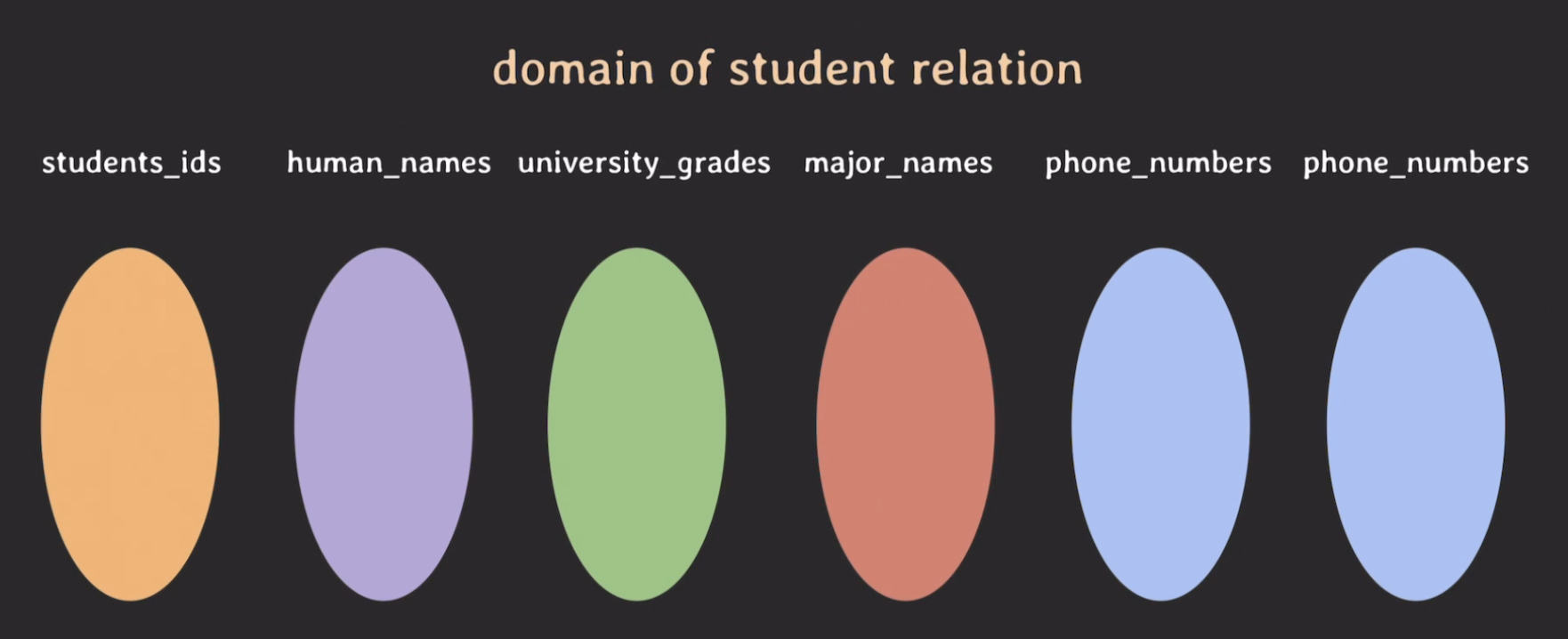
• students_ids : 학번 집합, 7자리 integer 정수
• human_names: 사람 이름 집합, 문자열
• university_grades : 대학교 학년 집합, {1, 2, 3, 4}
• major_names : 대학교에서 배우는 전공 이름 집합
• phone_numbers : 핸드폰 번호 집합
  • phone_numbers가 두 개인 경우는 혹시 모를 상황에 대비해 비상 연락망도 넣은거임

속성 (attribute) : domain이 relation에서 맡은 역할의 이름

동일한 domain이 같은 relation에서 여러 번 사용되는 것은 사용되는 목적(역할)이 다르다. 그래서 이 역할이 다름을 표시해주기 위해 relational data model에서는 속성(attributes)이라는 개념이 등장한다.

attribute 추가하기

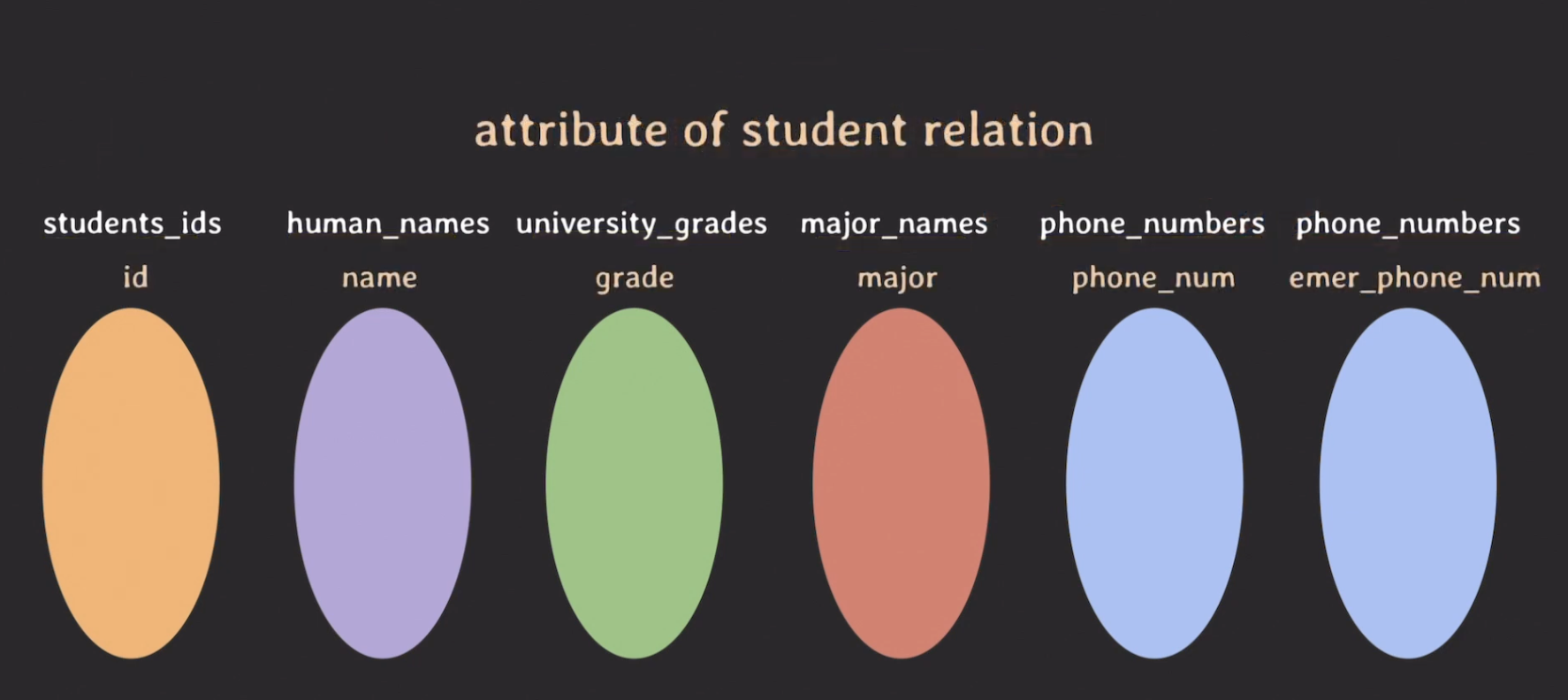
• 속성(attribute)은 각각의 도메인들이 릴레이션에서 어떤 역할을 수행하는 지, 수행하는 역할에 이름을 붙여주는 것이다.

튜플 (tuple) : 각 attribute의 값으로 이루어진 리스트

tuple 표시하기

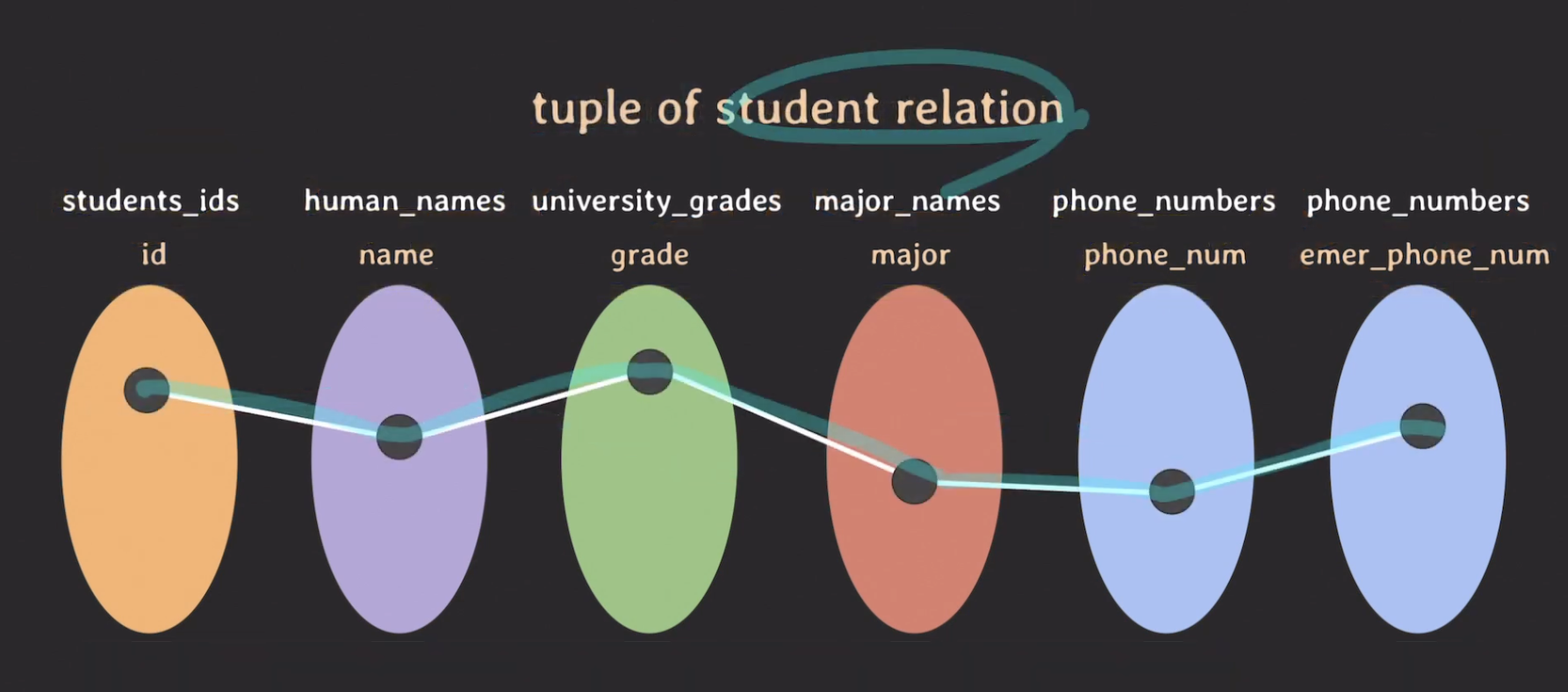
• domain은 어떤 값들로 이루어진 집합이라고 했으니까 각각의 domain마다 값들이 있을 것
• 이 값 중에서 실제로 data가 존재하는 튜플(tuple)들이 있을 것

근데, 사실 relational data model에서 relation을 표현할 때 이렇게 그림으로 잘 표현하지 않고 테이블로 표현하는 것이 익숙할 것이다. 그래서 그냥 relation을 추상적으로, 전체적으로 table이라고 생각하자.

student relation in relational data model

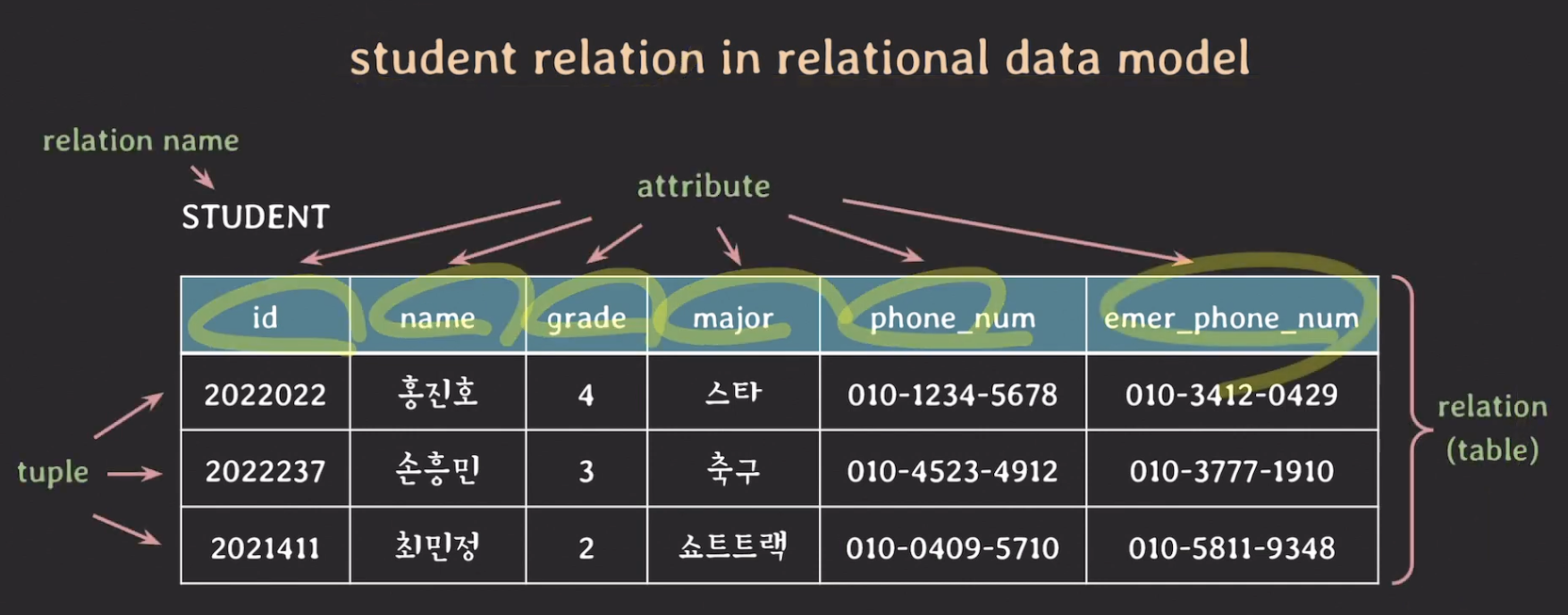
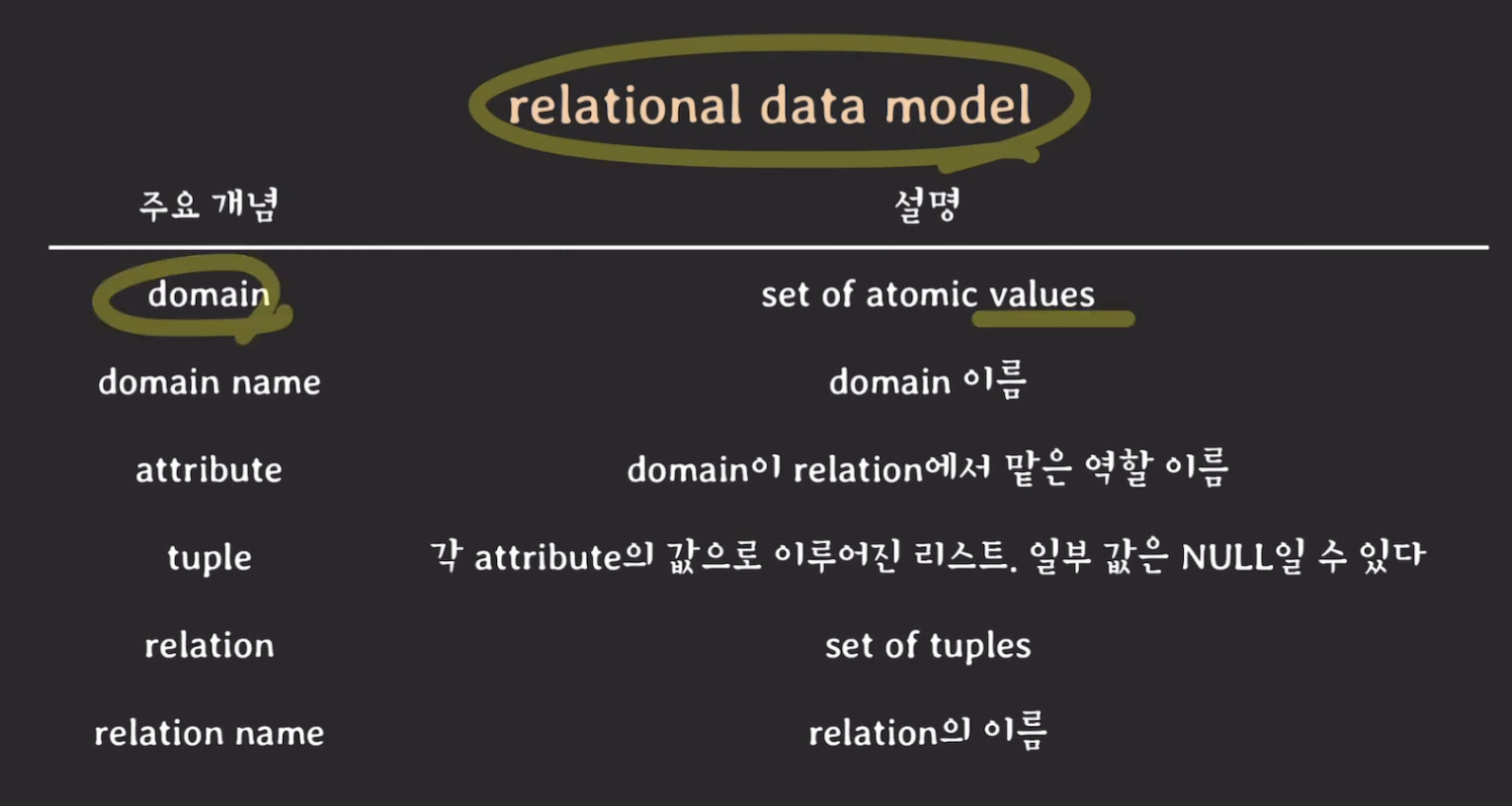
• set of atomic values는 집합이 더 이상 나눌 수 없는 값들로 이루어져야 한다는 제약사항을 의미

• relation의 구조를 나타냄
• relation 이름 + attributes 리스트로 표시
• ex) STUDENT(id, name, grade, major, phone_num, emer_phone_num)
• attributes와 관련된 constraints도 포함

• relation schema에서 attributes의 수
• ex) STUDENT(id, name, grade, major, phone_num, emer_phone_num)
  • 속성이 총 6개니까 degree는 6
  • 차원의 수는 6이라고도 함

위에서는 relation을 추상적으로 전체적으로 테이블 자체를 릴레이션이라고 생각하라고 했는데, relation을 relation state라고 생각할 수도 있다. 이것은 튜플들의 집합을 의미한다.

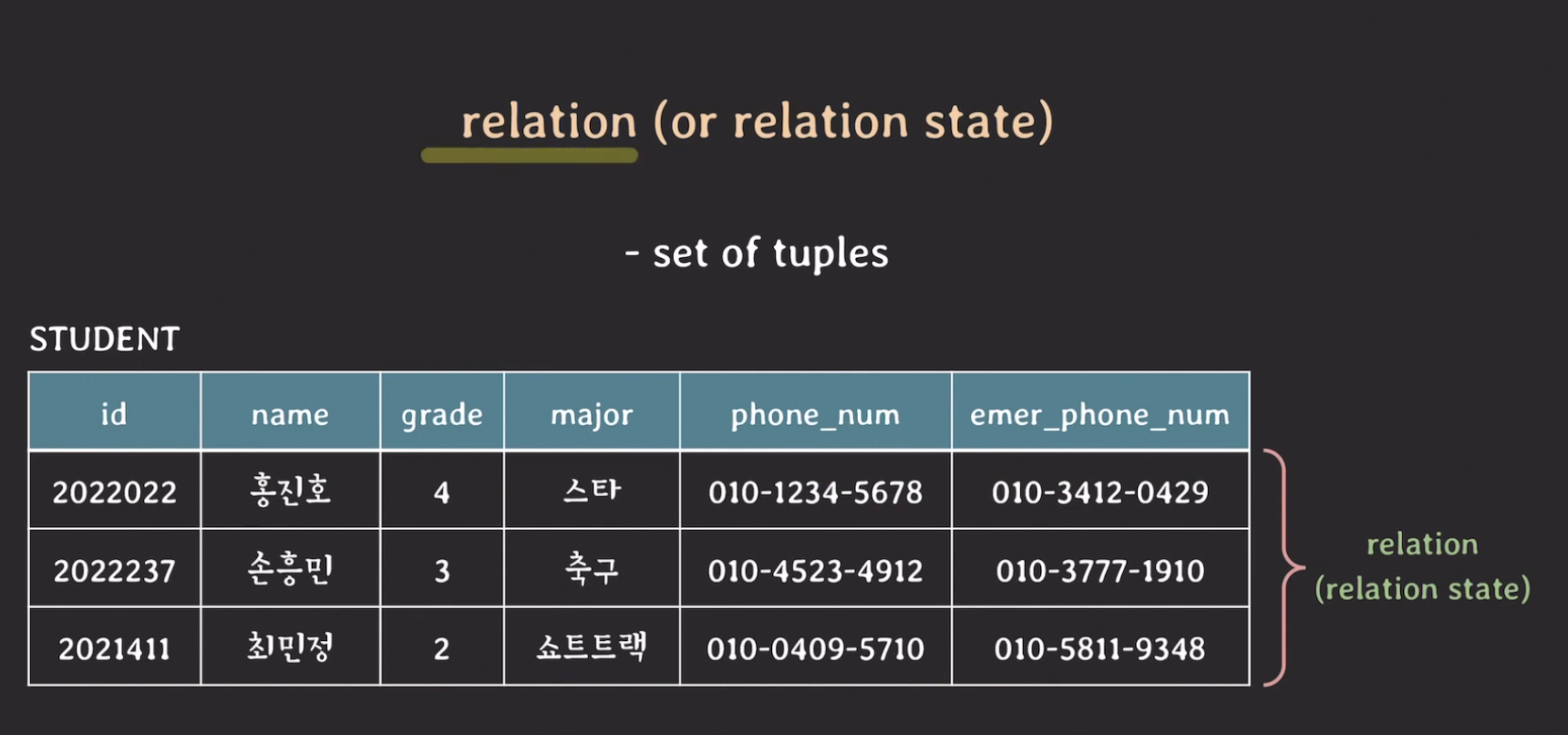
• 즉, 추상적이고 전체적인 테이블 자체를 relation이라고 하는 것이 아니라 실제 존재하는 데이터에 한정해서 relation이라고 할 수도 있다는 의미
• 도큐먼트를 보면서 추상적인, 개념적인 의미의 relation을 의미하는 것인지, 혹은 튜플들의 집합으로써의 relation을 의미하는 것인지 잘 파악하도록 하자.

관계형 DB (relational database)

• relational data model에 기반하여 구조화된 database
• relational database는 여러 개의 relations으로 구성된다.

관계형 DB 스키마 (relational database schema)

• 릴레이션 스키마들의 집합 + 무결성 제약조건들의 집합
• (relation schemas set + integrity constraints set)

• 중복된 튜플을 가질 수 없다.
• 속성의 부분집합을 key로 가진다.
• 튜플의 순서는 중요하지 않다.
• 하나의 릴레이션에서 속성 이름 중복 불가능
• 하나의 튜플에서 속성 순서 중요하지 않음
• 속성은 아토믹 해야함

1. 중복 튜플 불가 : relation은 중복된 tuple을 가질 수 없음 (relation is set of tuples)

• relation의 개념 자체가 튜플들의 집합이니까
• 집합은 중복을 허용하지 않으니까 !!

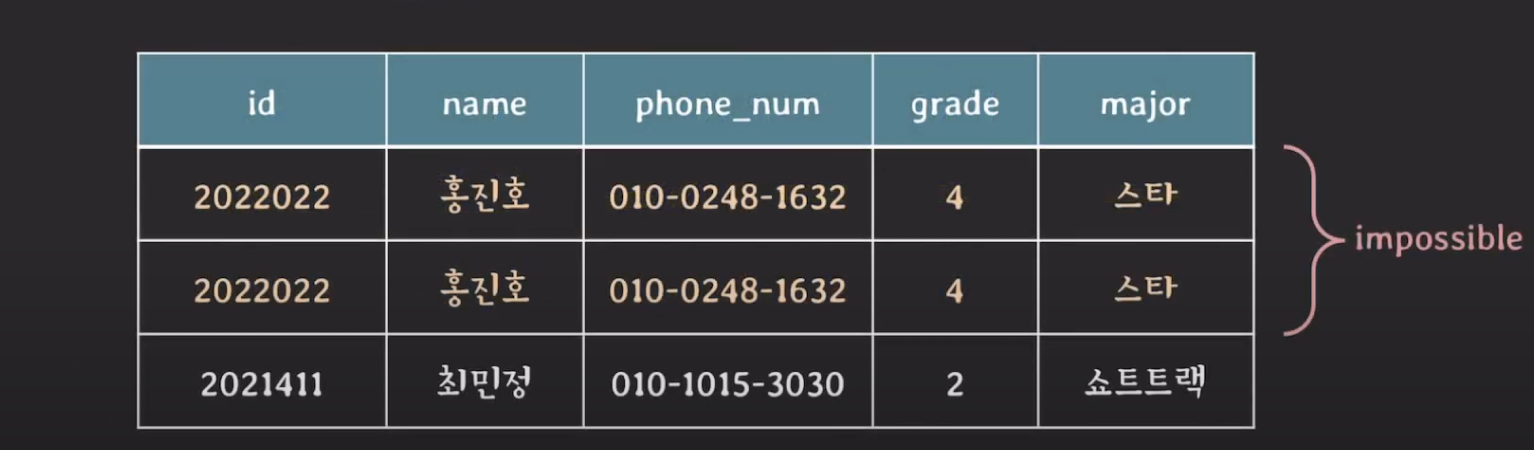
2. 속성의 부분집합 key : relation의 tuple을 식별하기 위해 attribute의 부분 집합을 key로 설정함

• 속성 중 id라는 것을 통해서 튜플을 유니크하게 구분할 수 있음

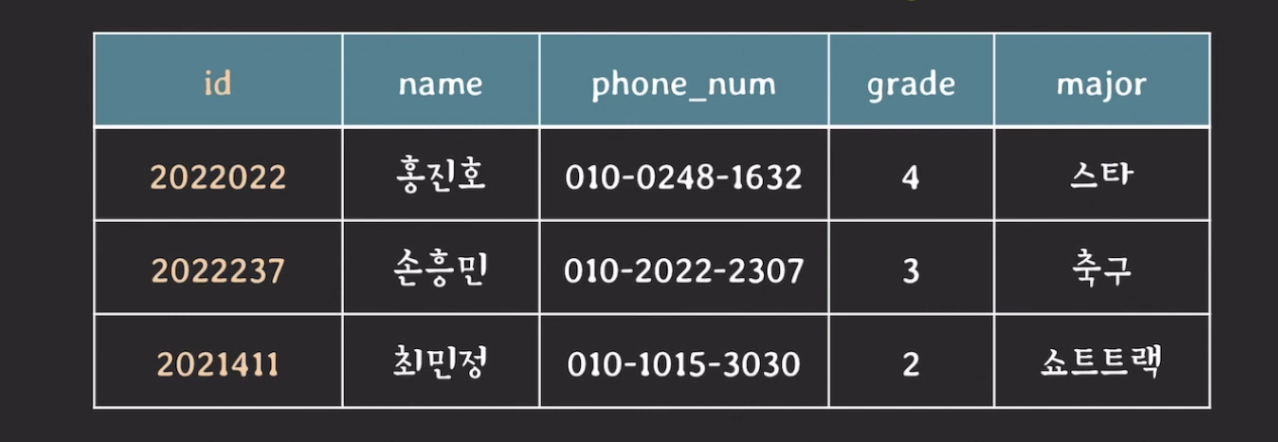
3. 튜플 순서 상관 X : relation에서 tuple의 순서는 중요하지 않음

• 튜플 간에 순서가 바뀌어도 릴레이션의 의미가 바뀌지 않음
• 즉, 튜플을 표시할 때 순서를 정하는 방법에 여러가지가 있을 수 있다.
  • ex) id 기준, name 기준, 등등

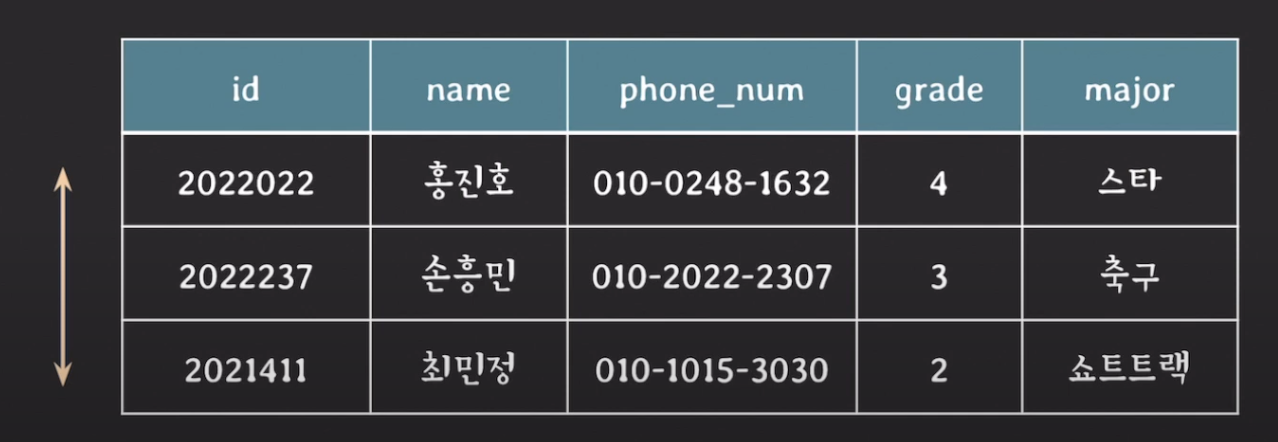
4. 속성 이름 중복 불가 : 하나의 relation(table)에서 attribute의 이름은 중복되면 안됨

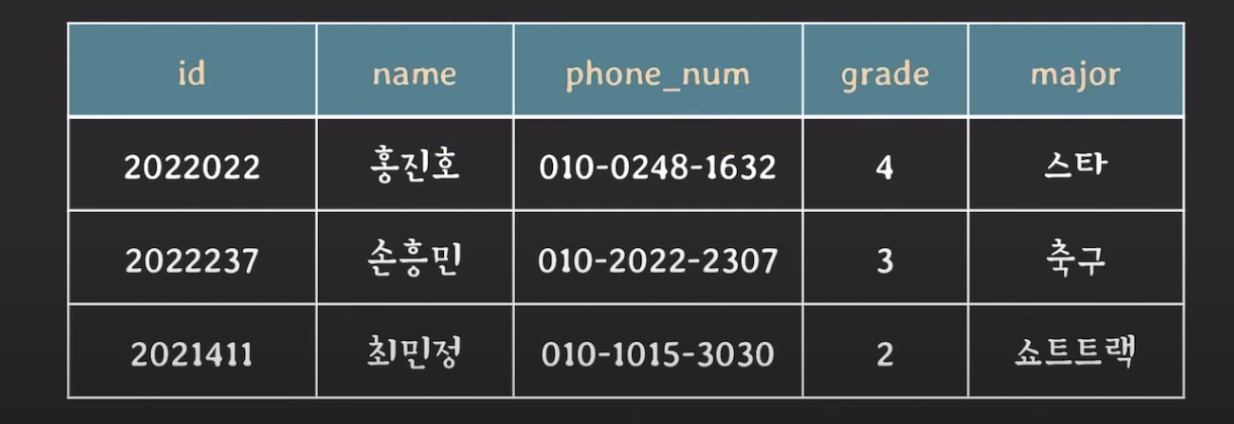
5. 속성 순서 중요 X : 하나의 tuple에서 attribute의 순서는 중요하지 않음

6. 속성 atomic 해야함 : attribute는 atomic 해야 한다. (composite or multivalued attribute 허용 안됨)

• atomic은 더이상 나눌 수 없는, 원자적인 이라는 의미
• 현재 address라는 속성은 서울특별시 / 강남구 / 청담동 세 가지로 쪼갤 수 있는 속성이다.
  • 이렇게 여러 가지 속성이 묶인 것을 복합 속성(composite attribtue)이라고 함.
  • 따라서, atomic 하지 않으니까 쪼개야 한다.
• 현재 major라는 속성은 컴공, 디자인 이라는 2가지 값을 동시에 가진다.
  • 이런 것을 다중값 속성(multivalued attribute)이라고 함.
  • 따라서, atomic 하지 않으니까 쪼개야 한다.

NULL의 의미는 여러 가지가 있다. 따라서 최대한 NULL을 사용하지 않는 것이 좋다.

• 값이 존재하지 않음
• 값이 존재하지만 아직 그 값이 무엇인지 알지 못함
• 해당 사항과 관련 없음

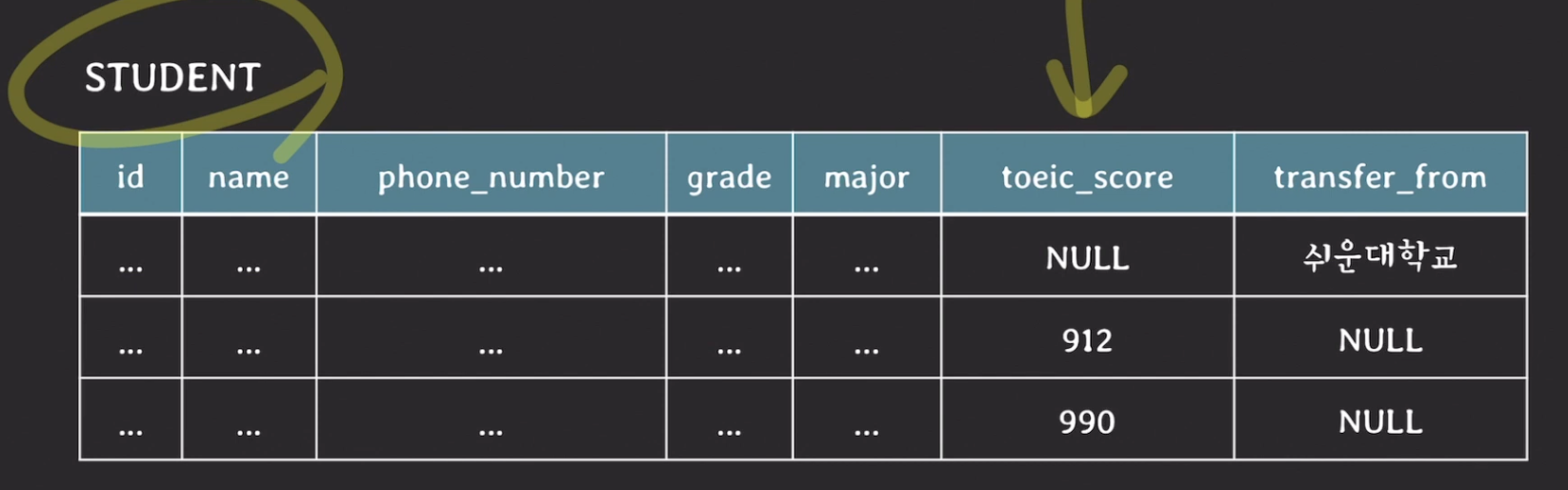
• toeic_score (토익점수)
  • 아직 토익을 치지 않아서 값이 NULL 일 수 있음
  • 시험을 쳤지만 제출 안했을수도
  • 제출했는데 누락돼서 업데이트 안됐을 수도
• transfer_from (편입정보)
  • 아예 편입하지 않았을 수도, 해당사항 없음
  • 편입 했는데 아직 업데이트 안됐을 수도

슈퍼키 (super key) : relation에서 tuples를 unique 하게 식별할 수 있는 attributes set

• ex) PLAYER(id, name, team_id, back_number, birth_date) 릴레이션에서 슈퍼키
• {id, name, team_id, back_number, birth_date}
  • 릴레이션의 정의 자체가 튜플들로 이루어진 집합이니까 중복자체를 허용하지 않아서 전체 attributes set 자체로 superkey가 될 수 있음
• {id, name} , {name, team_id, back_number} .. 기타 등등

후보키 (candidate key) : 어느 한 attribute라도 제거하면 unique하게 tuples를 식별할 수 없는 슈퍼키(super key)

• 편하게 key라고 부르기도 하고 minimal superkey라고 부르기도 함
• ex) PLAYER(id, name, team_id, back_number, birth_date) 릴레이션 에서 후보키
• {id}
  • id는 이미 attribute가 1개니까 제거할 수 없음, 후보키
• {team_id, back_numer}
  • 이 둘 중 하나라도 없애면 각각 하나하나는 유니크하게 튜플들을 식별할 수 없음, 후보키

개인키 (primary key) : relation에서 tuples를 unique하게 식별하기 위해 선택된 후보키(candidate key)

• ex) PLAYER(id, name, team_id, back_number, birth_date) 릴레이션 에서 개인키
• {id} 혹은 {team_id, back_number} 둘 중 하나를 개인키로 선택
• 보통 attributes 수가 적은 경우를 pk로 선택 많이함. 여기서는 {id} 선택
• pk는 보통 밑줄 그어서 표시

유일키 (unique key) : 개인키(primary key)가 아닌 후보키(candidate keys)

• 대체키(alternate key) 라고도 부름
• ex) PLAYER(id, name, team_id, back_number, birth_date) 릴레이션 에서 유일키
• id가 pk로 선택된 경우에 유일키(=대체키) 는 {team_id, back_number}

외래키 (foreign key) : 다른 relation의 개인키(primary key)를 참조하는 attributes set

• ex) PLAYER(id, name, team_id, back_number, birth_date)
• ex) TEAM(id, name, manger)
• 여기서 외래키(foreign key)는 PLAYER의 {team_id}

제약(constraints)은 관계형 데이터베이스(relational database)의 relations들이 언제나 항상 지켜줘야 하는 제약 사항을 의미한다.

• 제약조건을 두는 이유는 데이터베이스가 일치된 형태로, 데이터의 일관성을 보장하기 위해 사용하는 개념이다.

묵시적 제약조건 (Implicit constraints) : 관계형 데이터 모델 자체가 가지는 제약조건

• relation은 중복되는 tuple을 가질 수 없음
• relation 내에서는 같은 이름의 attribute를 가질 수 없음

스키마-기반 제약조건 (schema-based constraints) : 주로 DDL을 통해 스키마에 직접 명시할 수 있는 제약조건

• 명시적 제약조건(explicit constraints)라고도 부름
• schema-based constraints는 아래와 같이 여러 종류가 있다.
  • domain constraints
  • key constraints
  • NULL value constraint
  • entity integrity constraint
  • referential integrity constraint

도메인 제약조건 (domain constraints)

• attribute의 value는 해당 attribute의 domain에 속한 value여야 한다.
• 100학년이라는건 말이 안되니까

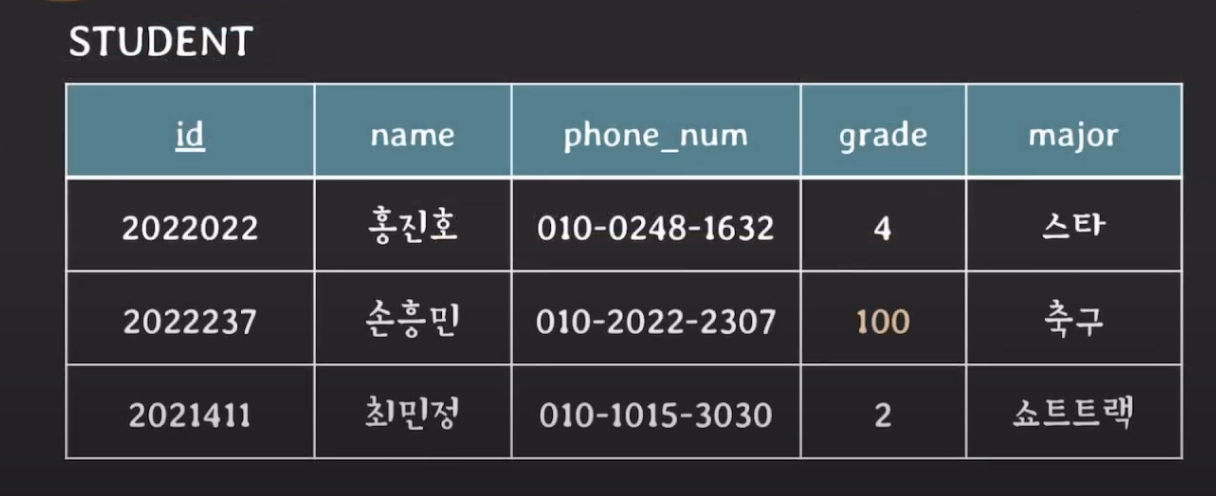
키 제약조건 (key constraints)

• 서로 다른 tuples는 같은 value의 key를 가질 수 없다.

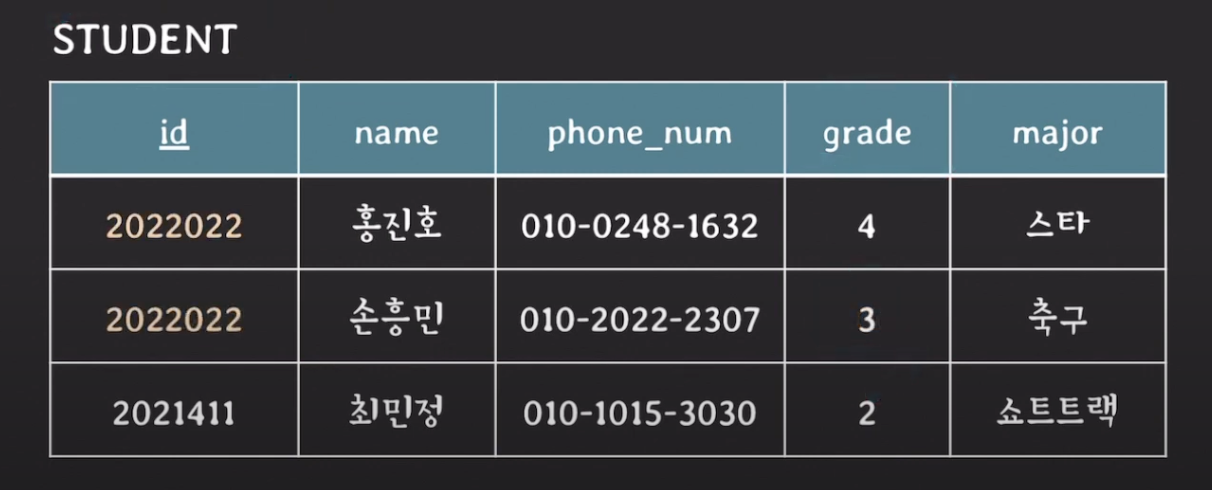
널 값 제약조건 (NULL value constraint)

• attribute가 NOT NULL로 명시됐다면 NULL을 값으로 가질 수 없다.

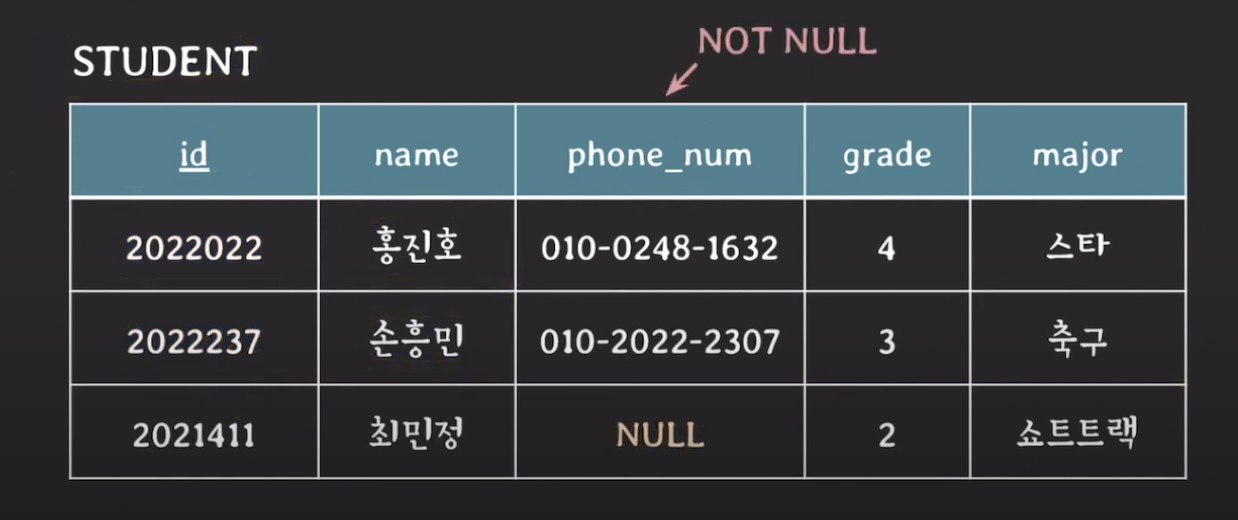
엔티티 무결성 제약조건 (entity integrity constraint)

• primary key는 value에 NULL을 가질 수 없다.

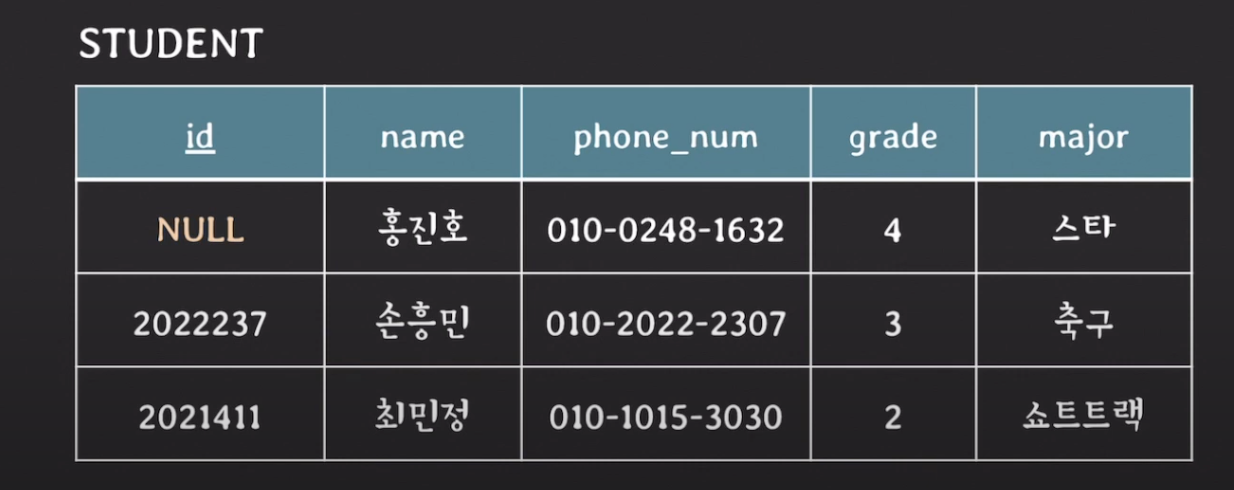
참조 무결성 제약조건 (referential integrity constraint)

• FK와 PK와 도메인이 같아야 하고 PK에 없는 values를 FK가 값으로 가질 수 없다.