08. 이진탐색트리 BST

Last updated - 2024년 11월 21일 Edit Source

유튜버 쉬운코드 님의 데이터 구조 강의를 정리한 내용

이진 탐색 트리 (binary search tree)

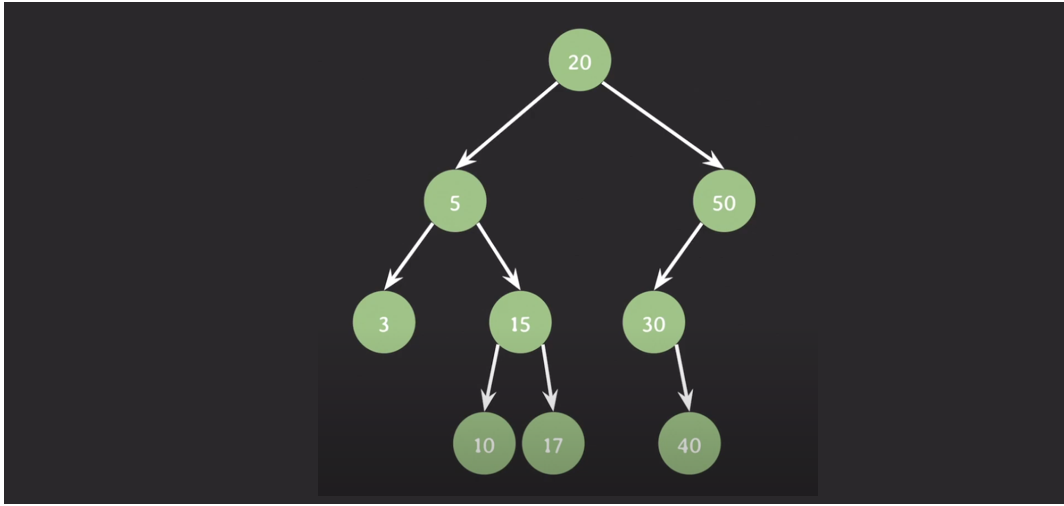
• 모든 노드의 왼쪽 서브 트리는 해당 노드의 값보다 작은 값들만 가짐
• 모든 노드의 오른쪽 서브 트리는 해당 노드의 값보다 큰 값들만 가짐
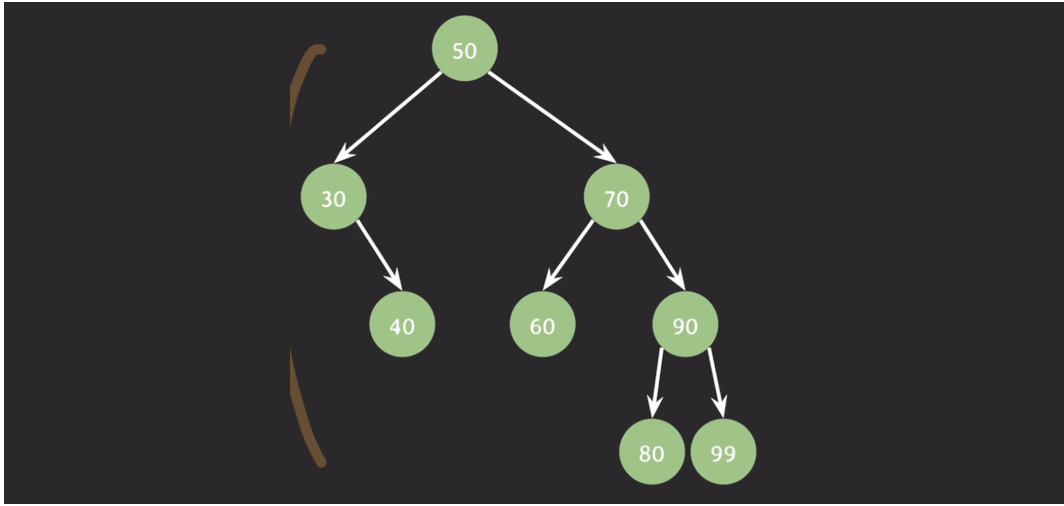
• 이진 탐색 트리의 최소값 : 트리의 가장 왼쪽에 존재
  • 왼쪽 → 왼쪽 하니까 최소값 3
• 이진 탐색 트리의 최대값 : 트리의 가장 오른쪽에 존재
  • 오른쪽 1번밖에 안됨. 최대값 50

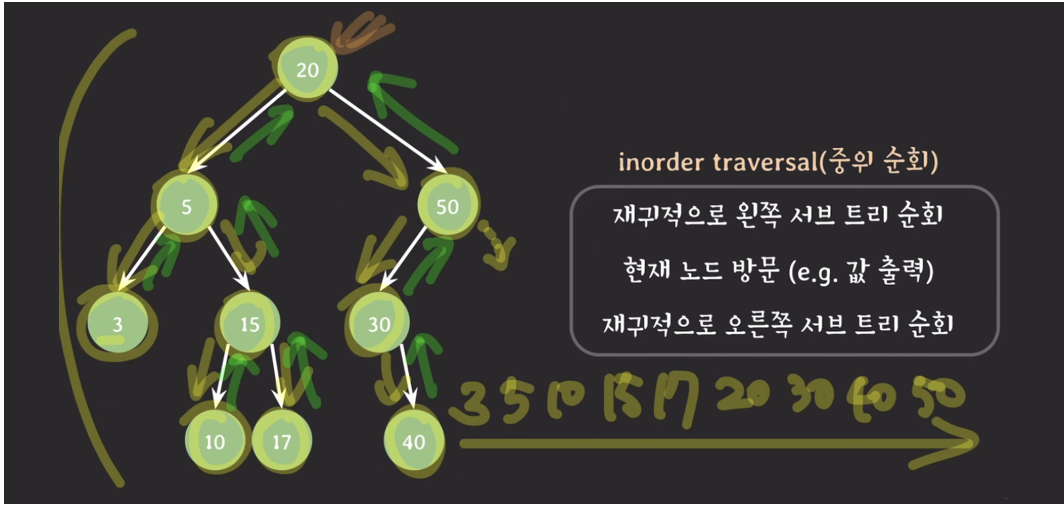
중위 순회 (inorder traversal)

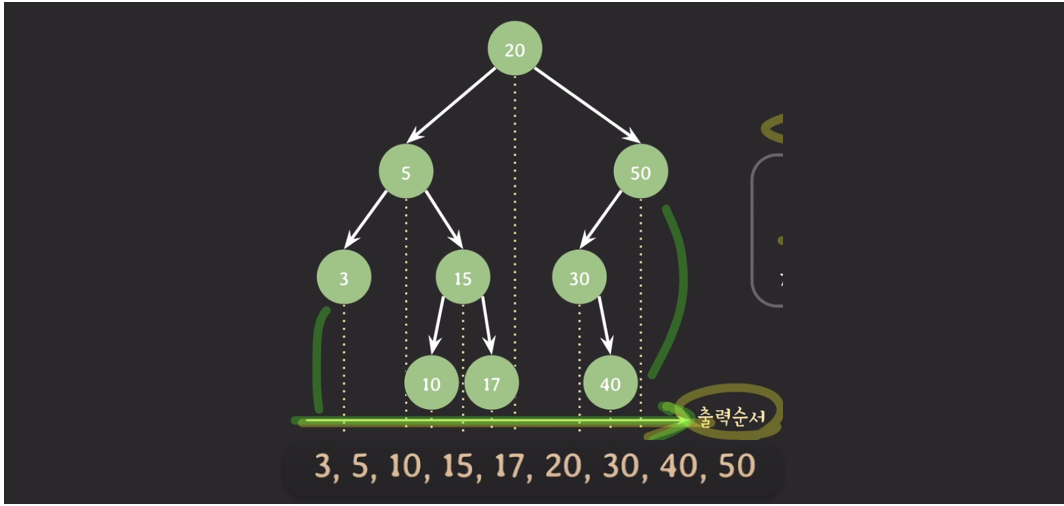
• 재귀적으로 왼쪽 서브 트리 순회
• 현재 노드 방문 (ex. 값 출력)
• 재귀적으로 오른쪽 서브 트리 순회
• 결과적으로 출력은 크기 순서로 나열됨

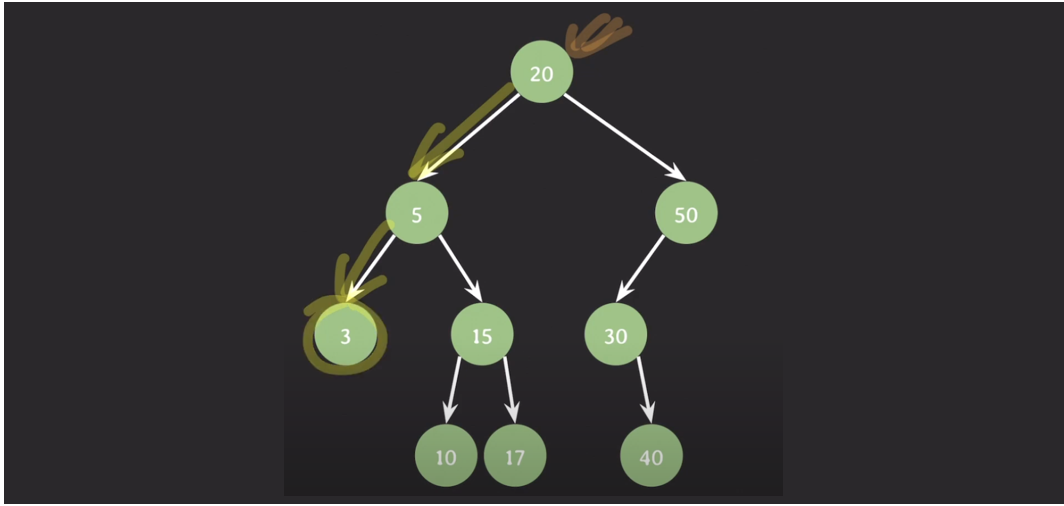
1. 출발은 항상 루트노드, 재귀적으로 왼쪽 서브트리 순회

2. 더이상 갈 왼쪽이 없으니까 현재 노드 방문 (여기서는 3번 노드)

3. 오른쪽으로 가려고 하니까 현재 노드의 오른쪽이 없음, 3번 노드의 할일은 끝

4. 5번 노드로 가면 왼쪽 서브트리 순회는 이미 끝난 상태

5. 현재 노드 방문하여 5번 노드 출력

6. 오른쪽 서브트리 순회, 15번은 다시 왼쪽으로

7. 10번 노드는 더이상 없음. 그러니까 다시 10번 출력

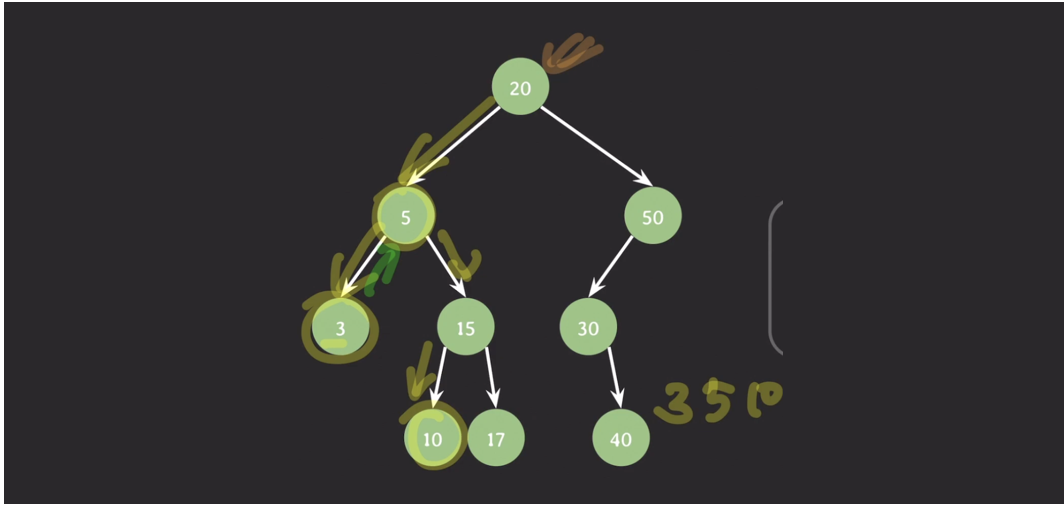
결국 반복하면 아래와 같이 결과가 나옴

전위 순회 (preorder traversal)

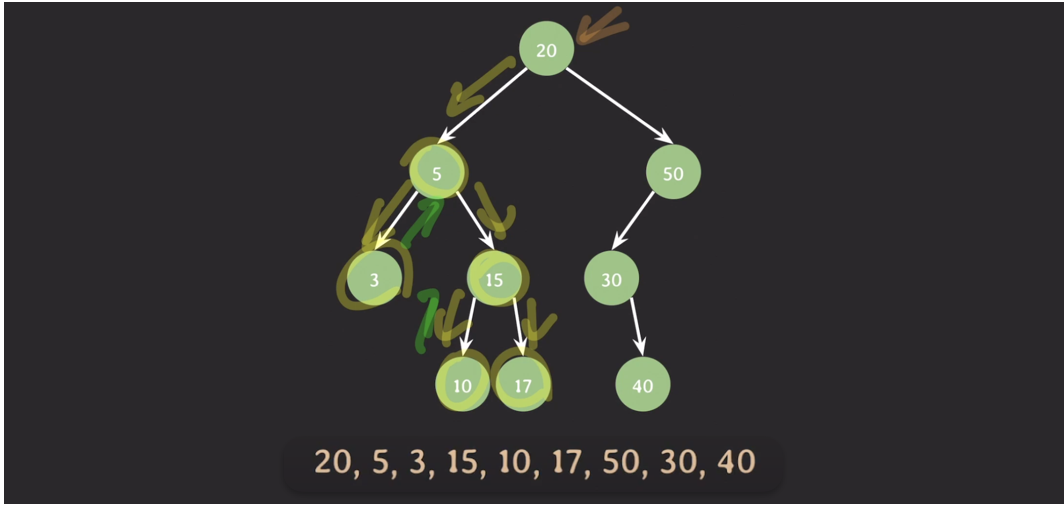
• 현재 노드 방문 (ex. 값 출력)
• 재귀적으로 왼쪽 서브 트리 순회
• 재귀적으로 오른쪽 서브 트리 순회

후위 순회 (postorder traversal)

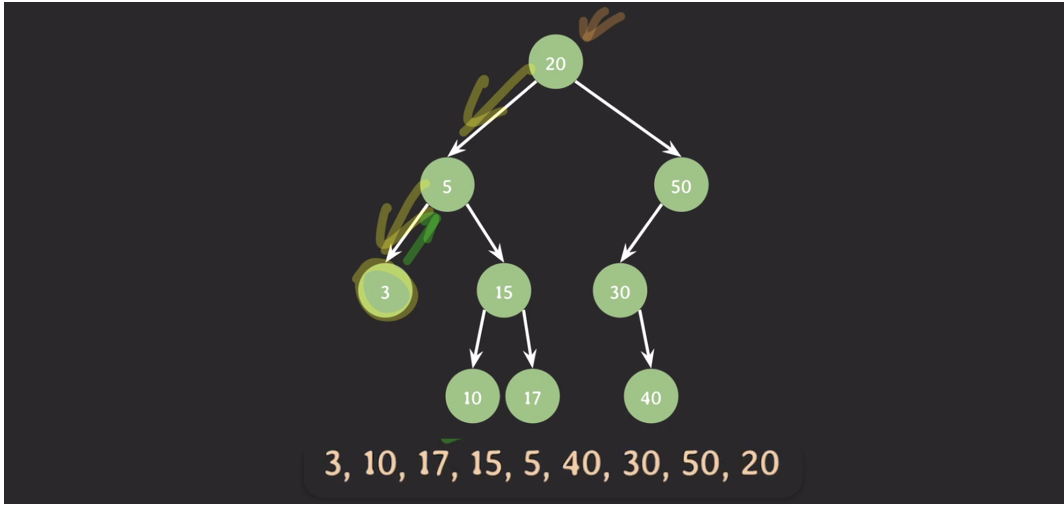
• 재귀적으로 왼쪽 서브 트리 순회
• 재귀적으로 오른쪽 서브 트리 순회
• 현재 노드 방문 (ex. 값 출력)

노드의 후임자 (successor)

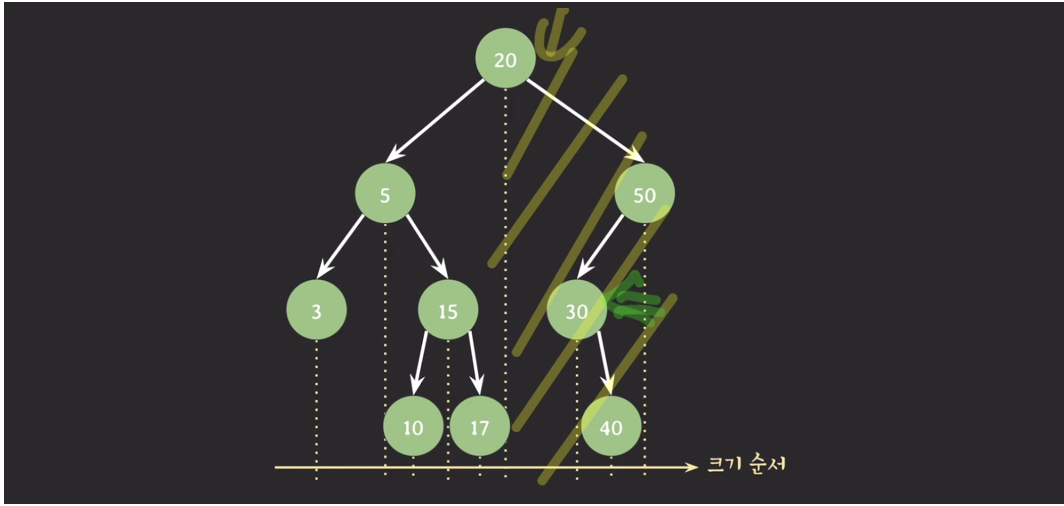
• 해당 노드보다 값이 큰 노드들 중에서 가장 값이 작은 노드
• ex) 20의 successor : 30
• ex) 17의 successor : 20
• ex) 10의 successor: 15

노드의 선임자 (predecessor)

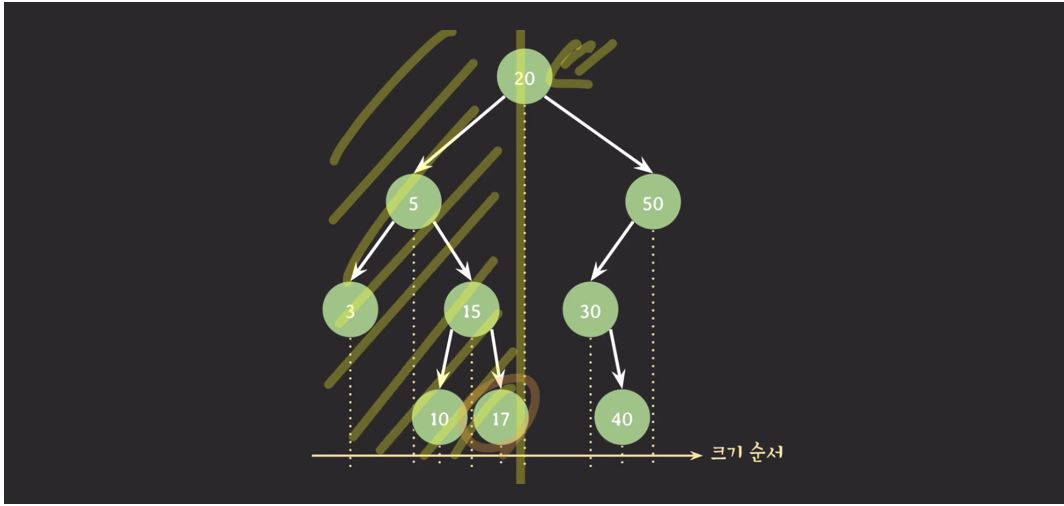
• 해당 노드보다 값이 작은 노드들 중에서 가장 값이 큰 노드
• ex) 20의 predecessor : 17
• ex) 10의 predecessor : 5
• ex) 40의 predecessor : 30

삽입

• 그냥 값이 크면 오른쪽, 작으면 왼쪽 이거만 기억하고 넣으면 됨

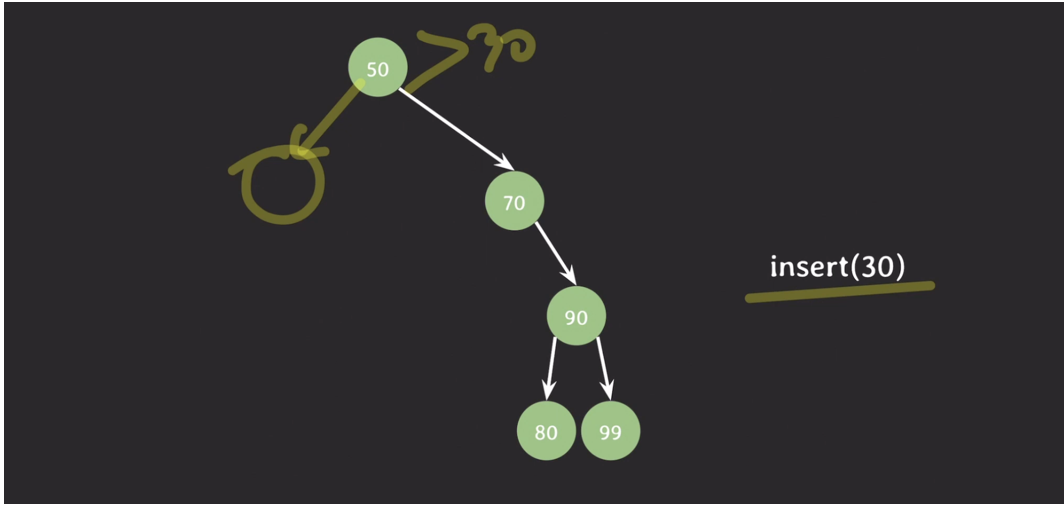
삭제

• 삭제하려는 노드가 있는지 먼저 검색
• 있으면 삭제
• 즉, 삭제는 검색이라는 작업이 동반됨

자녀가 없는 노드 삭제

• 삭제될 노드를 가리키던 레퍼런스를 가리키는 것이 없도록 처리

자녀가 하나인 노드 삭제

• 삭제될 노드를 가리키던 레퍼런스를 삭제될 노드의 자녀를 가리키게 변경

자녀가 둘인 노드 삭제

• 삭제될 노드의 오른쪽 서브트리에서 제일 값이 작은 노드가 삭제될 노드를 대체
• 만약, 왼쪽 서브트리로 정했다면 제일 값이 큰 노드가 삭제될 노드를 대체하면 됨

ex) 20 삭제

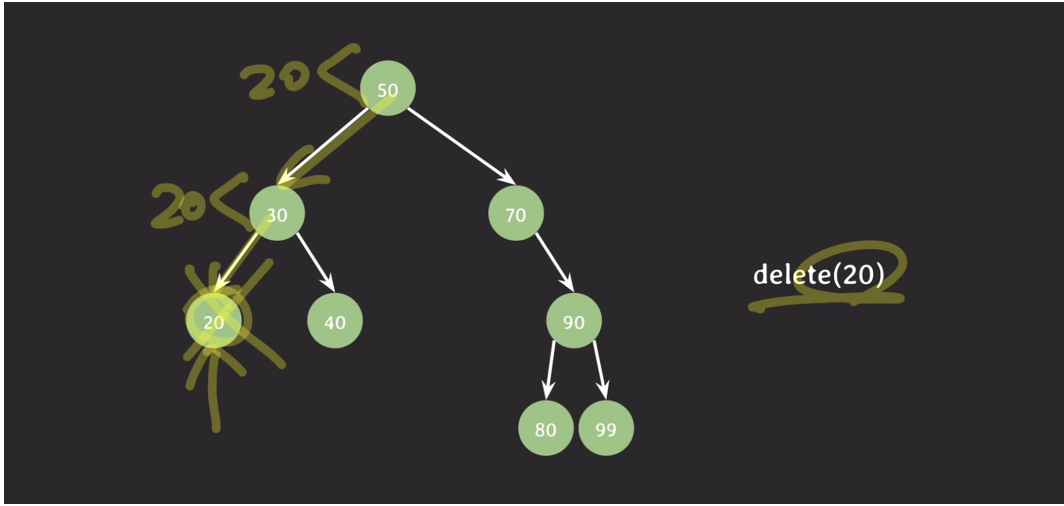
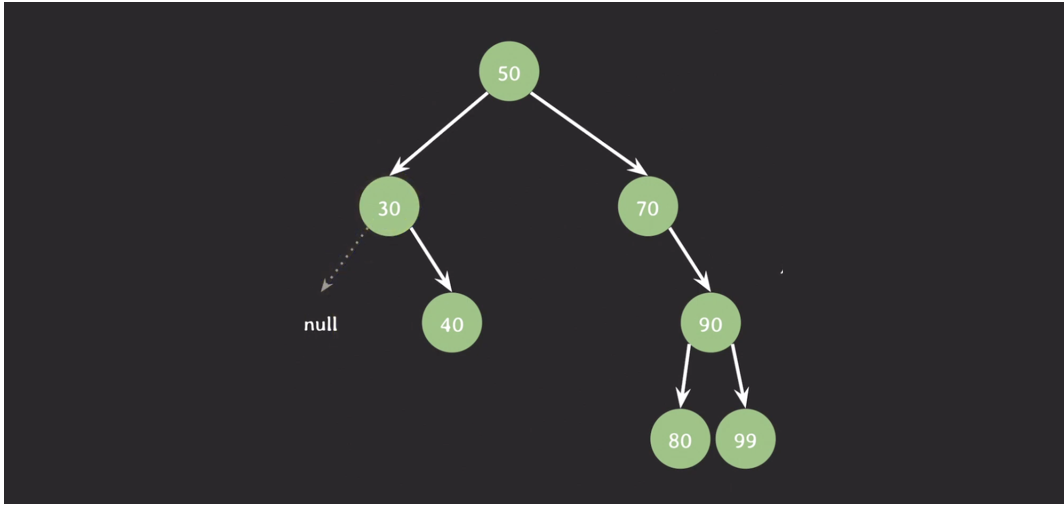
ex) 30 삭제

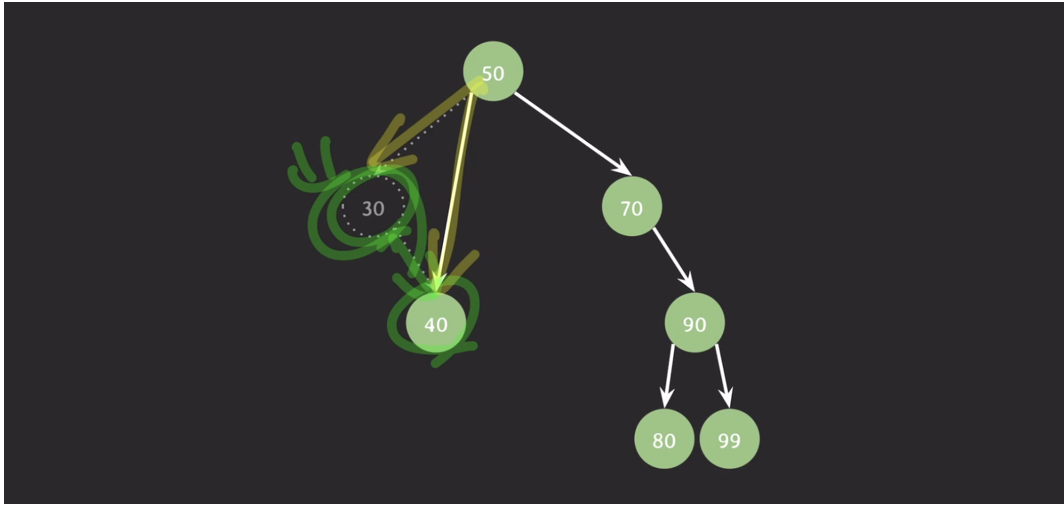
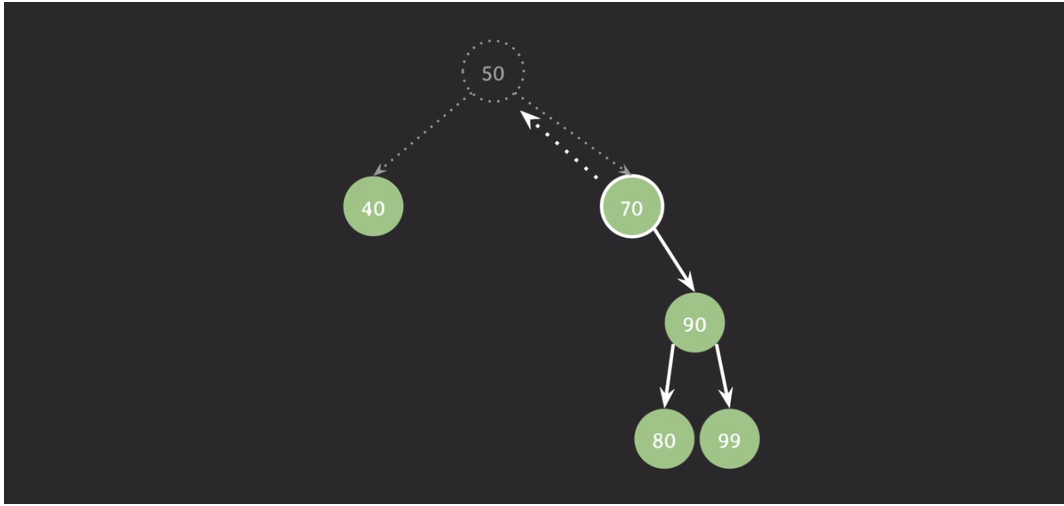
ex) 50 삭제

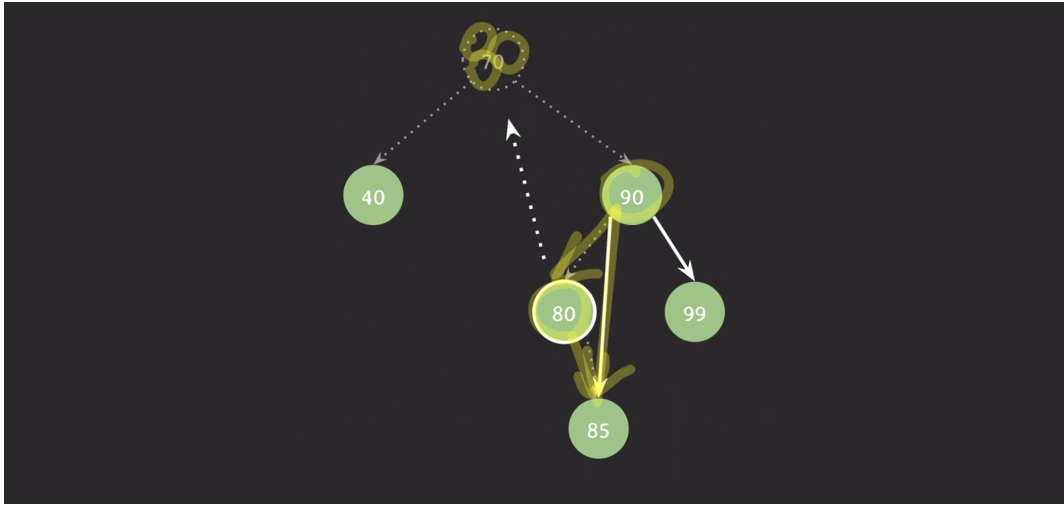
ex) 기타

best case

• insert : $\Theta (1)$
• delete : $\Theta (1)$
• search : $\Theta (1)$

average case

• insert : $O (\log N)$
• delete : $O (\log N)$
• search : $O (\log N)$
• 왼쪽이던 오른쪽이던 선택한 쪽만 집중하면 점근적으로 사이즈를 절반씩 줄여나갈 수 있음

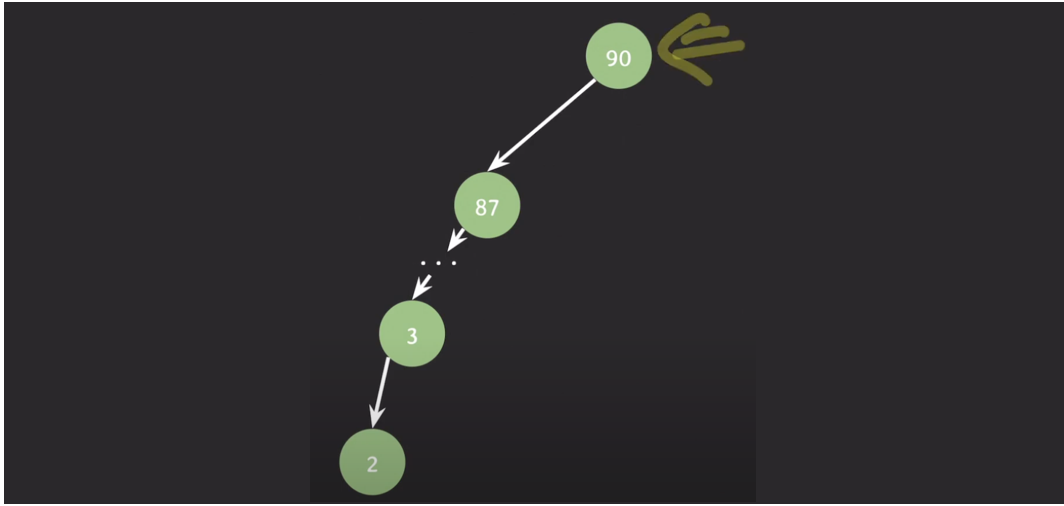
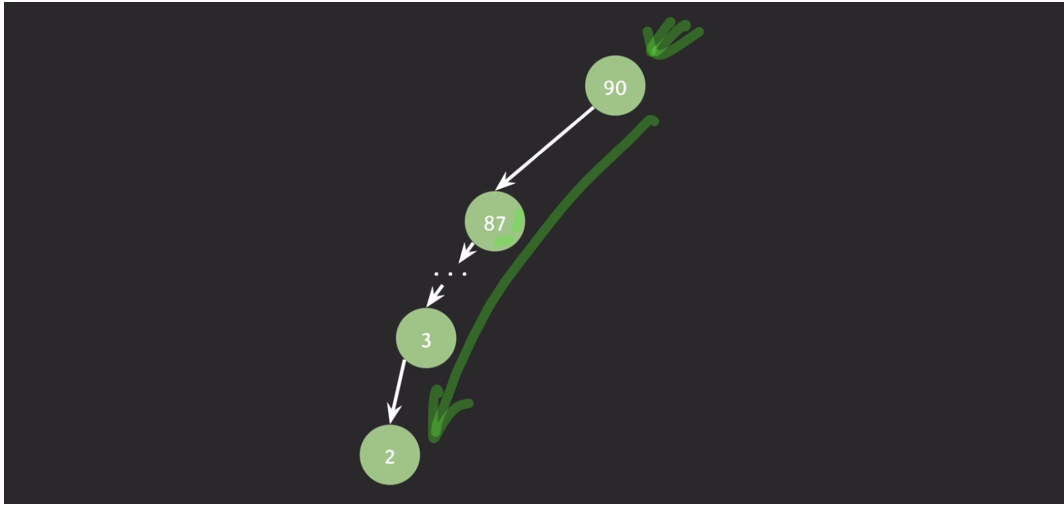
worst case

• insert : $\Theta (N)$
• delete : $\Theta (N)$
• search : $\Theta (N)$
• ex) 1을 넣어야 한다면 모든 노드 확인해야함

이진탐색트리 장점

• 삽입 / 삭제가 유연 (레퍼런스만 재조정하면 되니까)
• 값의 크기에 따라 좌우 서브트리가 나눠지기 때문에 삽입/삭제/검색이 (보통은) 빠르다
• 값의 순서대로 순회 가능 (정렬된 형태로 접근 가능하다는 말)

이진탐색트리 단점

• 트리가 구조적으로 한쪽으로 편향되면 삽입/삭제/검색 등등 수행시간이 악화됨
• 이 문제를 해결하기 위해 스스로 균형을 잡는 이진탐색트리가 사용됨
  • ex) AVL 트리, Red-Black 트리
  • 얘네는 worst case 에서도 $O(\log N)$으로 처리됨