Dev Uni

  • Home
  • About
  • Brain
  • Project
    • Search IconIcon to open search

    Search⌘ + k

    Ch02 - 시간복잡도

    Last updated - 2024년 11월 21일 Edit Source

      패스트캠퍼스 핵심유형 20개로 한 번에 끝내는 알고리즘 코딩테스트 with Java 강의를 정리한 내용

      # 시간 복잡도

      • 입력 크기와 알고리즘 간의 관계
      • 알고리즘의 복잡도를 나타내는 지표 중 하나
      • 입력 크기에 대해 프로그램의 동작시간을 가늠해볼 수 있는 수단
      • Big-O / Big-Omega / Big-Theta 표기법
        • 주로 Big-O를 사용, 정의된 입력 데이터 중 가장 최악의 상황을 포함한 시간의 상한선

      코딩테스트에서의 시간복잡도

      • 보편적으로 문제마다 시간 제한이 주어짐
      • 시간 제한이 1초라면, 최악의 테스트케이스에서도 해당 시간 내에 프로그램이 답을 구할 수 있어야 한다.
      • 시간 제한을 넘어가면 시간 초과뜨고 프로그램 종료
      • 편의상 1초에 약 1억 번 연산을 기준으로 소요시간을 가늠할 수 있다.
        • 상수/최적화 등에 따라 시간 복잡도가 1천만 밖에 되지 않아도 1초를 넘기거나 시간 복잡도로 10억이 넘어도 1초 안에 실행될 수 있다.
        • 절대적 기준이 아닌 상대적 지표

      적합한 알고리즘 선택 기준

      • 정답을 구하는 알고리즘이 여러 개인 경우
        • 시간이 넉넉하다? => 구현이 쉬운 방법
        • 제한이 있다? => 시간/메모리상으로 효율적인 방법

      배열의 최댓값을 구하는 예시

      1. 반복문 이용 => O(n)
      1
2
3
4
5
6
7
8

      public static int getMaxIntArray(int[] arr) {
	int maxValue = arr[0];
	for (int i = 1; i < arr.length; i++) {
		if (arr[i] > maxValue)
			maxValue = arr[i];
	}
	return maxValue;
}
      1. 정렬 메서드 이용 => O(n log n), O(n2)
      1
2
3
4

      public static int getMaxIntArray(int[] arr) {
	Arrays.sort(arr);
	return arr[arr.length - 1];
}

      예를 들어, 입력 n이 1000만이라고 하자. => 1번 방법 선택

      만약, 시간 제한이 크지는 않다면 ? n이 작다면? => 편한 방법 고르기


      1. (번외) 스트림
      1
2
3

      public static int getMaxIntArray(int[] arr) {
	return Arrays.stream(arr).max.getAsInt();
}

      # 시간복잡도를 통한 추론

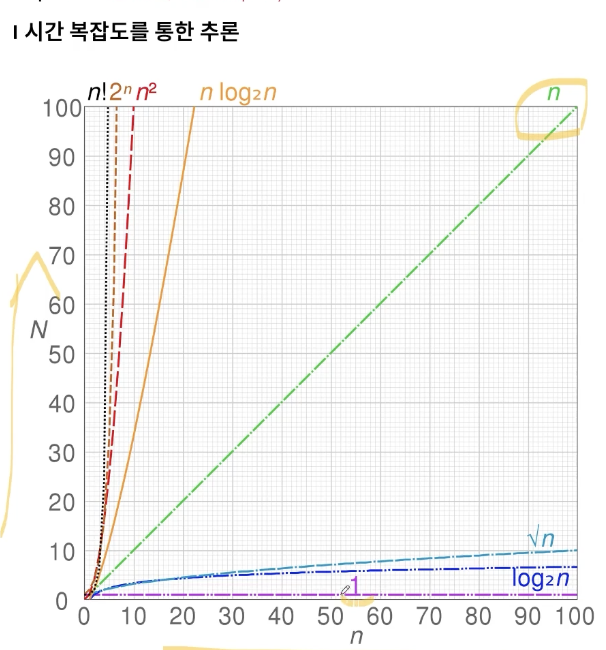
      O(1) < O(log2n) < O(n) < O(n log2n) < O(n2) < O(2n)


      N의 범위시간 복잡도
      N <= 10 ~ 11O(N!)
      N <= 24 ~ 25O(2N)
      N <= 300 ~ 500O(N3)
      ==N <= 5,000 ~ 10,000==O(N2)
      N <= 50,000 ~ 100,000O(N 루트 N)
      ==N <= 100,000 ~ 1,000,000==O(N log2N)
      ==N <= 10,000,000==O(N)
      N개의 데이터가 입력이 아닌
      범위 등으로 주어질 때      		O(루트 N) , O(log N), O(1)

      # 10158번 문제

      • 해설은 강의내용을 참고하도록 하자.
      • 내가 생각한 포인트는 x축과 y축을 별개로 나눠서 따로 구하는 것까지는 생각했음
      • 그러나, 시간제한 때문에 반복문을 아예 안쓰는걸로 생각해서 더 나아가지 못했다.
        • 반복문을 사용하면 시간제한이 O(N)이 되버리니까 당연히 시간초과

      여기에서 개미가 움직이는걸 보다보면 주기성이 있다는 것을 확인할 수 있음.

      => 주기성이 있다 = 반복된다 = 모듈러(%) 연산으로 연산 횟수를 낮출 수 있다. = 반복문을 사용하더라도 시간복잡도가 O(N)이 아니게 할 수 있다.


      1. 기본적인 입력값은 받아왔음
       1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

      import java.util.*;  
import java.io.*;  
  
public class Main {  
    public static void main(String[] args) throws IOException {  
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));  
        StringTokenizer st = new StringTokenizer(br.readLine());  
        int w = Integer.parseInt(st.nextToken());  
        int h = Integer.parseInt(st.nextToken());  
        st = new StringTokenizer(br.readLine());  
        int x = Integer.parseInt(st.nextToken());  
        int y = Integer.parseInt(st.nextToken());  
        int t = Integer.parseInt(br.readLine());       
    }  
}

      1. 기초로직
        • w나 h에 이를 곱하는건 왔다갔다 하는거니까
        • 1시간에 1만큼 이동하니까, 거리 1을 1시간으로 볼 수도 있겠네
          • 따라서, 시작 위치가 (2, ?), w = 6 이었다고 하자.
          • (2 ~ 6) 4만큼 + (6 ~ 0) 6만큼 + (0 ~ 2) 2만큼 => 12
          • 12번마다 처음으로 돌아오네! 주기가 12
            • 여기서 처음은 위치와 가는 방향까지 동일한거 의미함
        • 그러면, 시간이 30이라고 하면 (시간 % 주기)를 하면 나머지니까 마지막 위치 나오겠네.
       1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

      // 시간복잡도 O(2W)
int dx = 1;
int timeX = t % (2 * w);
while (timeX-- > 0) {
	if (x == w)
		dx = -1;

	else if (x == 0)
		dx = 1;

	x += dx;
}


       1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

      // 시간복잡도 O(2H)
int dy = 1;
int timeY = t % (2 * h);
while (timeY-- > 0) {
	if (y == h)
		dy = -1;
		
	else if (y == 0)
		dy = 1;
		
	y += dy;
}

      처음에 문제 범위가 2 <= W, H <= 40,000 , 1 <= T <= 200,000,000 이었다. 따라서 기초로직의 시간복잡도는 O(max(W, H)) 이기 때문에 통과할 것이다.

      하지만, W, H가 40,000보다 더 커지면 어떻게 할거냐? 시간 복잡도 더 줄여보자


      1. 시작을 시작위치가 아니라 0에서부터 시작
        • 아까 위치 1만큼 1시간이라고 했으니까 그냥 시간으로 볼 수도 있다고 했다.
        • 그러면 0부터 시작하고 (현재위치 + 걸린시간) 하면 되지않을까?
       1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

      int dx = 1;
int timeX = (x + t) % (2 * w);
while (timeX-- > 0) {
	if (x == w) 
		dx = -1;
		
	else if (x == 0)
		dx = 1;

	x += dx;
}


       1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

      int dy = 1;
int timeY = (y + t) % (2 * h);
while (timeY-- > 0) {
	if (y == h) 
		dy = -1;
		
	else if (y == 0)
		dy = 1;

	y += dy;
}

      • 다음으로 더 나아가서 0부터 시작했고, 주기가 2W니까 가운데 W를 기점으로 값이 바뀌잖아? 이를 이용하면
      • x <= w이면 값 그대로 x좌표이다.
      • x > w이면 w를 만나 방향이 전환되므로 식을 세울 수 있다. w로부터 멀어지는데 현재 위치인 x와 w 만큼의 차이만큼 멀어짐!
        • w - (x - w)
        • 2w - x

       1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

      import java.util.*;  
import java.io.*;  
  
public class Main {  
    public static void main(String[] args) throws IOException {  
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));  
        StringTokenizer st = new StringTokenizer(br.readLine());  
        int w = Integer.parseInt(st.nextToken());  
        int h = Integer.parseInt(st.nextToken());  
        st = new StringTokenizer(br.readLine());  
        int x = Integer.parseInt(st.nextToken());  
        int y = Integer.parseInt(st.nextToken());  
        int t = Integer.parseInt(br.readLine());  
  
        int currentX = (t + x) % (2 * w);  
        int currentY = (t + y) % (2 * h);  
        if (currentX > w)  
            currentX = 2 * w - currentX;  
        if (currentY > h)  
            currentY = 2 * h - currentY;  
  
        System.out.println(currentX + " " + currentY);  
    }  
}
      • 이렇게 최종적으로 반복문을 쓰지않고 O(1)을 만들면서 문제를 끝낼 수 있다.

      Comment