수학
# 유클리드 호제법
최대공약수 (GCD, Greateast Common Division)
최소공배수 (LCM, Least Common Multiple)

- 두 수 A, B와 최대공약수 G, 최소공배수 L이라고 하면
AB = LG식이 성립
유클리드 호제법 : 최대공약수 GCD 찾는 방법
- A를 B로 나눈 몫을 Q라 하고, 나머지를 R이라고 하면
GCD(A, B) = GCD(B, R) - 자연수 A, B가 있을 때 A를 B로 나눈 나머지를 N이라고 하면 (
a % b == n) N이 0일 때 B가 바로 최대공약수 GCD 임을 이용하는 원리- N이 0이 아니라면, a에 b값을 넣고 다시 n을 b에 대입하여 재귀
- 기본적으로 a가 b보다 크다는 전제 !!!
- A를 B로 나눈 몫을 Q라 하고, 나머지를 R이라고 하면
- 프로그래머스에서 풀었던 재귀
- 유클리드 호제법 위키피디아에서도 이와 같이 품
| |
- 코드트리 단순 반복
| |
- 완전 쉬운 반복
- 최소공배수는
LCM = (n * m) / GCD
- 최소공배수는
| |
# 콜라스 추측
모든 자연수에 대하여, 짝수는 나누기 2, 홀수는 곱하기 3 + 1을 유한번 재귀하면 결국 최종적으로 1로 간다는 것. 아직까지 반례를 찾지 못했음
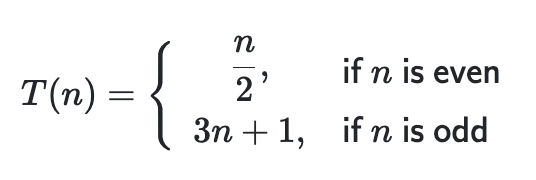
- 위키피디아 - 콜라스 추측
- 3n + 1 수열이라는 키워드도 봤음
# 피보나치 수열
첫 번째 원소 1, 두 번째 원소 1, 세 번째 원소 부터는 바로 직전 두 원소의 합인 수열

# 순열 조합

| |