비교정렬
# 비교정렬 개념
비교정렬 (Comparison sort) : 정렬 알고리즘의 일종으로 두 값을 비교하는 것에 기반하는 알고리즘
- 데이터 간 상대적 크기 관계만을 이용해서 정렬하는 알고리즘
- 대표적으로 버블정렬, 선택정렬, 삽입정렬, 합병정렬, 퀵정렬, 힙 정렬
- 메모리를 어떻게 쓰냐에 따라 내부 정렬, 외부 정렬, 제자리 정렬로 나뉨
- 두 값이 같을 때, 값이 어떤 순서로 정렬되는지에 따라 안정 정렬, 불안정 정렬로 나뉨
기본적으로 비교 정렬을 구현하는 방법에 있어서, 기본 정렬 알고리즘과 고급 정렬 알고리즘이 있다.
- 기본 정렬 알고리즘
- 시간 복잡도가 $O(n^2)$인 정렬 알고리즘
- 버블 정렬, 선택 정렬, 삽입 정렬
- 고급 정렬 알고리즘
- 시간 복잡도가 $O(n \log n)$인 정렬 알고리즘
- 합병 정렬, 퀵 정렬, 힙 정렬
# 비교정렬 한계
비교 정렬 알고리즘은 최악의 경우에 $O(n \log n)$보다 더 나은 성능을 낼 수 없다. 왜 이런 한계를 가지고 있을까?
비교 정렬 알고리즘은 추상적인 관점에서 모두 의사 결정 트리(Decision Tree) 로 볼 수 있다. 크냐, 작냐와 같은 특정한 기준(질문)에 따라 비교하여 원소를 구분하기 때문이다. a, b, c를 비교하는 것을 의사 결정 트리로 표현한 예시를 살펴보자.
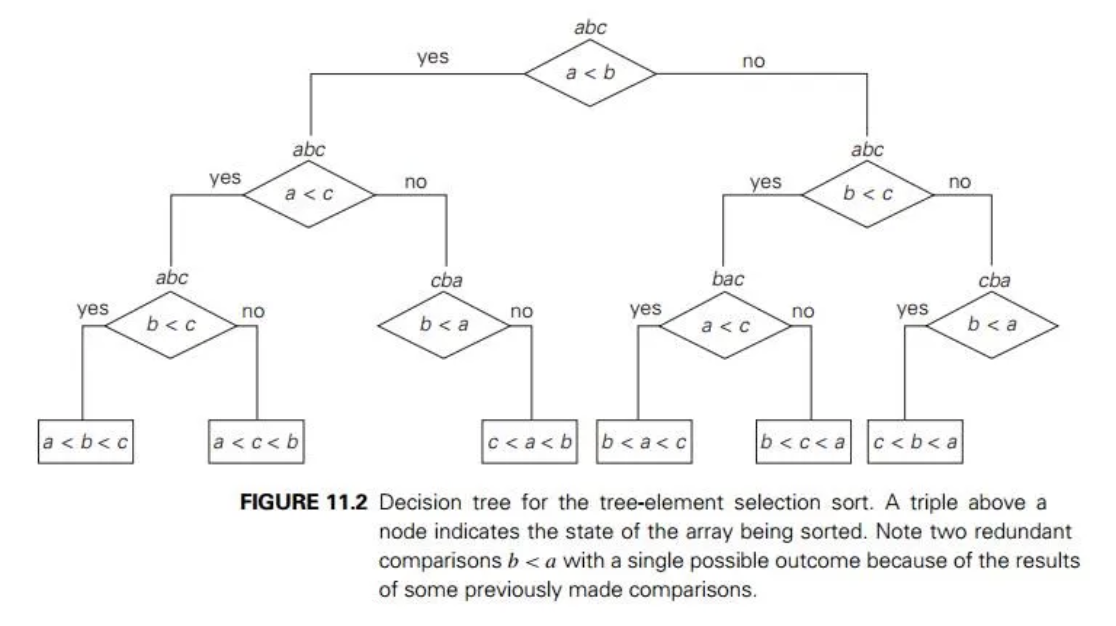
정렬 알고리즘의 실행은 루트에서부터 트리의 말단 노드(더이상 자식이 없는 트리, 리프 노트라고도 함)까지 경로를 따라가는 것에 대응한다. 즉, 루트 노드로부터 가장 먼 말단 노드까지 가는 경로의 길이가 최악의 경우의 비교 횟수를 나타내는 것이다. 이는 트리의 높이를 의미한다.
n개를 비교하는 의사 결정 트리의 가능한 모든 리프 노드의 개수는 $n!$개
- n개에 대한 모든 순열이 존재하기 때문
트리의 높이를 h라고 하면, 최대 리프의 개수는 이진 트리이므로 $2^h$개
도달 가능한 리프가 L개라고 하면 아래의 식이 성립
$$ n! <= L <= 2^h $$
- 양변에 로그($\log_2$)를 취하면
$$ \log 2^h <= \log L <= \log n! $$
$$ h <= \log(n!) $$
- $n!$을 스털링 근사하여 스털링 급수로 바꾸면 $n! \sim \sqrt{2\pi n} (\frac{n}{e})^n$
$$ n \log n <= h $$
따라서, 최악의 경우의 비교 횟수( = 트리의 높이, h)는 $O(n \log n)$보다 반드시 커야 한다. 이로 인하여, 비교 정렬 알고리즘은 최악의 경우 $O(n \log n)$보다 나은 성능을 낼 수 없다.
# 비교정렬 개선
그렇다면, 어떻게 더 최적으로 정렬할 수 있을까? 비교를 안하면 된다. 이에 해당하는 정렬은 Non-Comparison Sort (비교하지 않는 정렬)이다.