Dev Uni

  • Home
  • About
  • Brain
  • Project
    • Search IconIcon to open search

    Search⌘ + k

    퀵 정렬

    Last updated - 2023년 04월 26일 Edit Source

      # 퀵정렬 개념

      퀵정렬 (Quick Sort) : 분할 정복의 일종으로, pivot(기준)을 설정하여 이를 올바른 위치로 이동시키고 나머지 원소들을 두 개의 배열로 분할하여 재귀적으로 정렬시키는 알고리즘

      • pivot 앞에는 pivot보다 값이 작은 것, 뒤에는 pivot보다 값이 큰 것이 오도록 함
        • pivot을 선정하는 방식에 따라 속도 차이가 발생함. pivot을 선정하는 방식은 아직도 논문으로 나올만큼 정답이 없음
        • 그래서 보통 물리적으로 중간에 위치한 값을 pivot으로 많이 설정함
        • 합병정렬과 달리 배열이 불균등하게 분할된다. 운 좋으면 균등하게 될 수도 있음
        • Arrays.sort()가 내부적으로 듀얼-피봇 퀵소트를 사용함
      • 시간복잡도 : $O(n \log n)$
        • 최선 : $O(n \log n)$, 평균 : $O(n \log n)$, 최악 : $O(n^2)$
        • 최악때문에 오해하기 쉬운데, 퀵소트가 합병정렬보다 평균적으로 빠름
        • 실전에서 평균적으로 $O(n \log n)$보다 빠름
      • 공간복잡도 : $O(\log n)$
        • 재귀호출을 위한 스택프레임 공간
        • 최악의 경우 $O(n)$까지 갈 수도 있음. 그러나 보통은 $O(\log n)$
      • 안정성&제자리성 : 불안정 정렬(Unstable-sort), 제자리 정렬 (In-place sort)
        • 동일한 원소에 대하여 정렬 후 본래의 순서가 유지안됨 → 불안정
        • 기존 배열 이외의 추가적인 메모리를 거의 사용하지 않음 - 제자리

      첫 번째 원소를 무조건 pivot으로 선정하는 경우


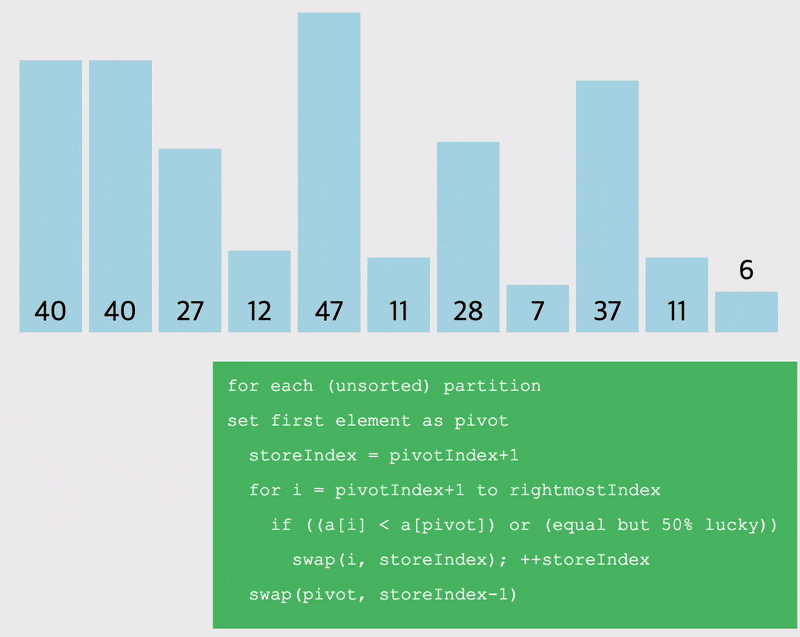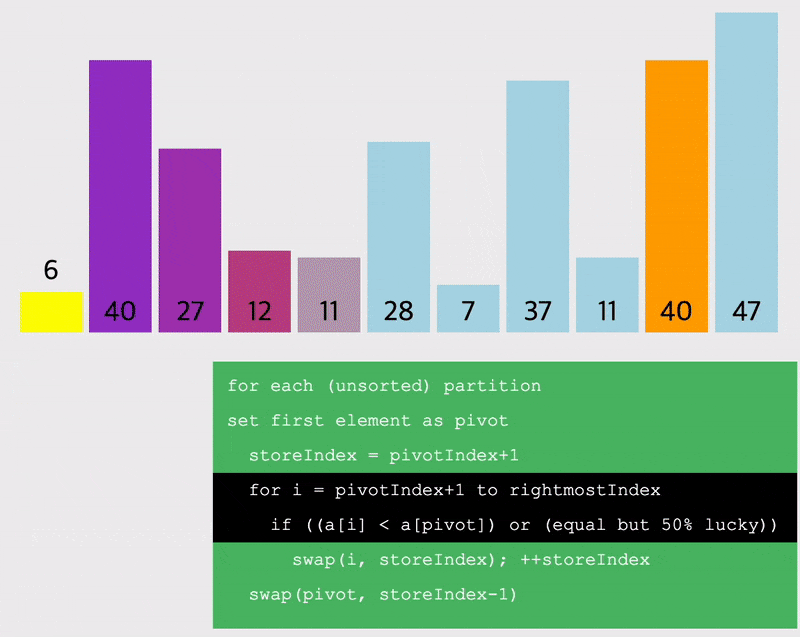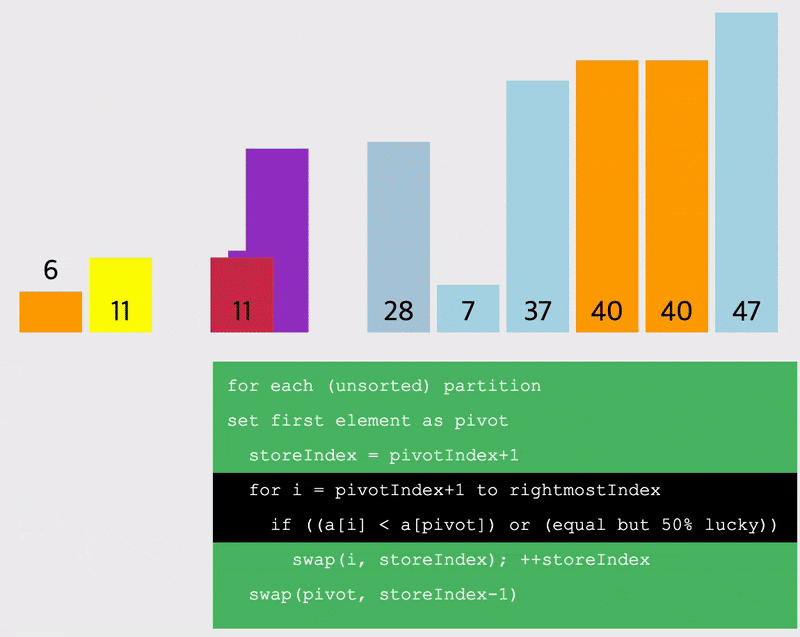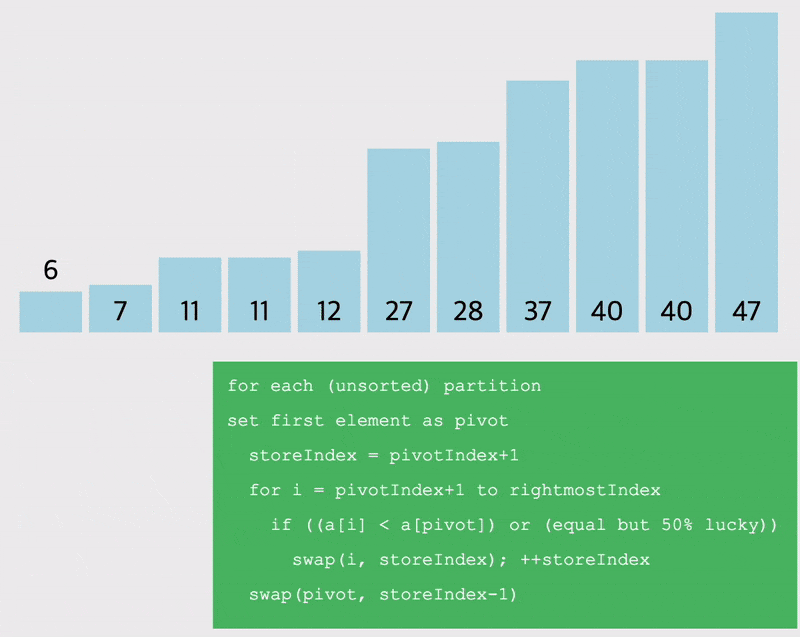
      pivot을 랜덤하게 선정하는 경우


      # 퀵정렬 시간복잡도

      희망편, 평균


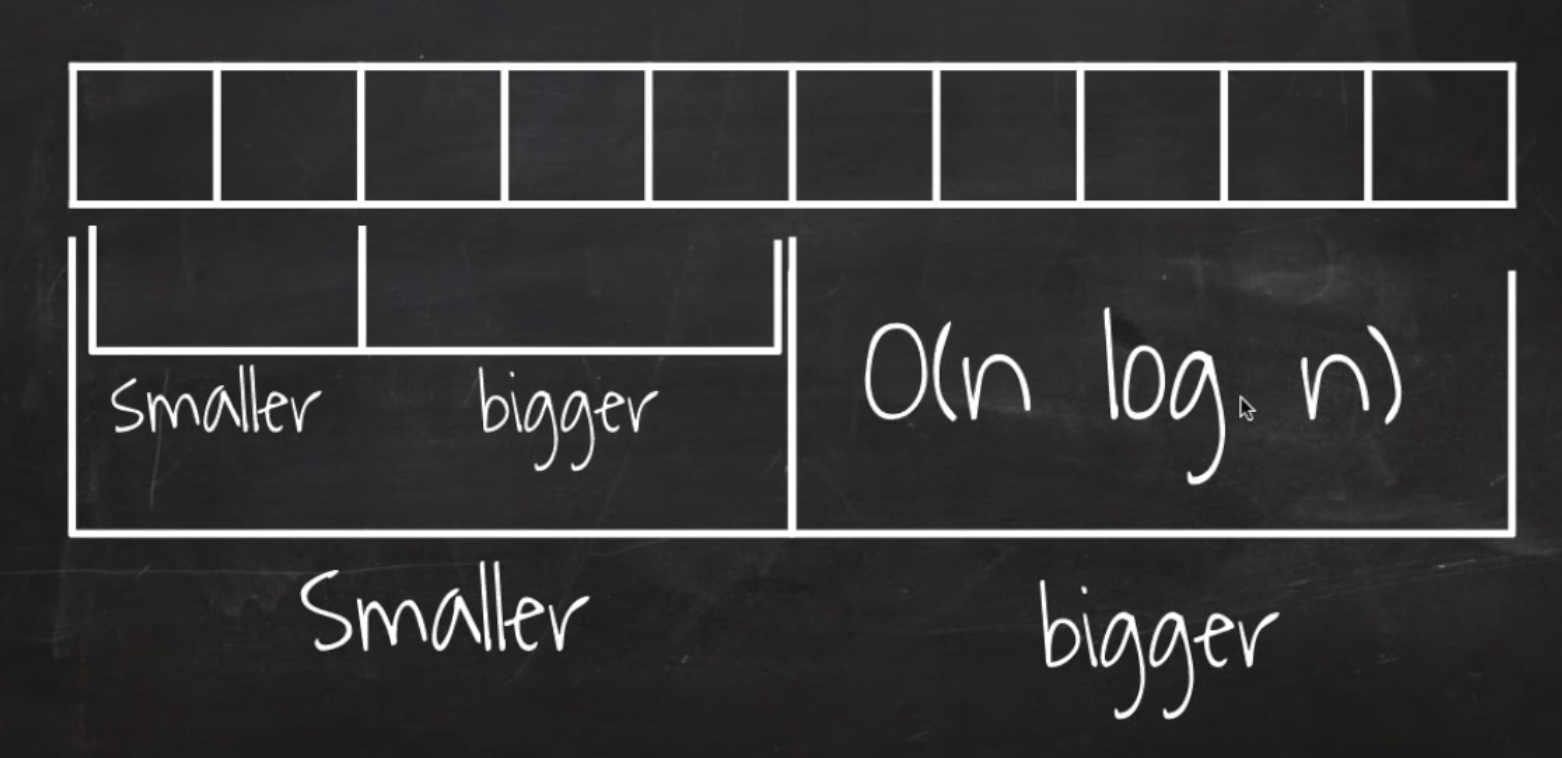
      절망편 : 하필이면 고른 pivot이 계속 최솟값이나 최댓값인 경우

      • 확률적으로 희박함


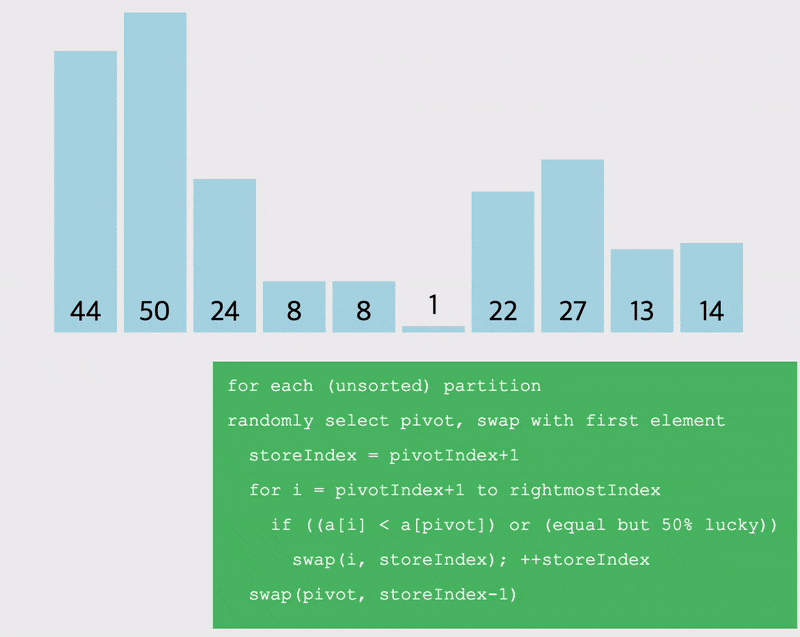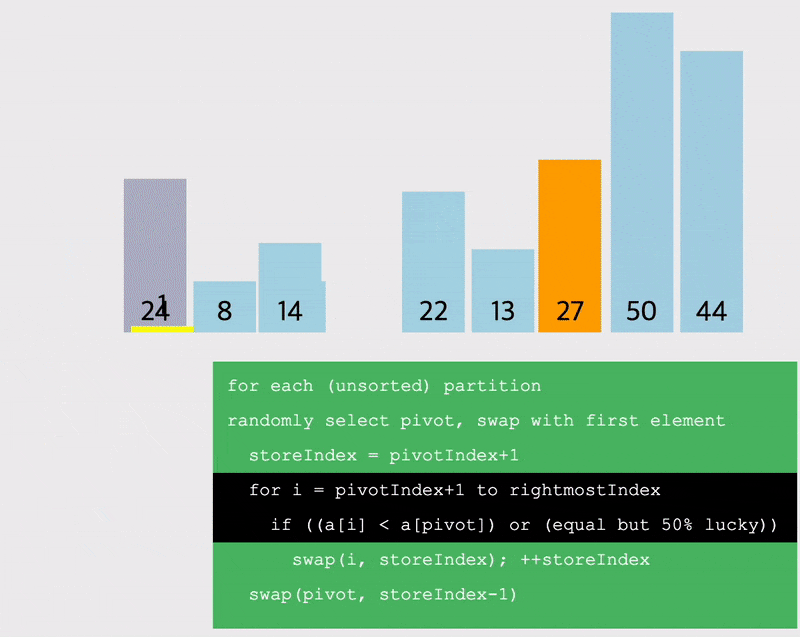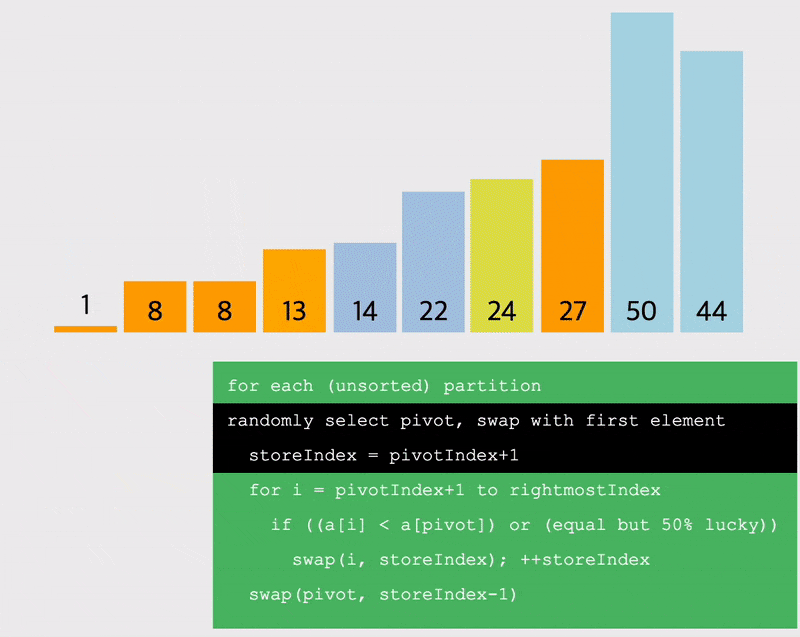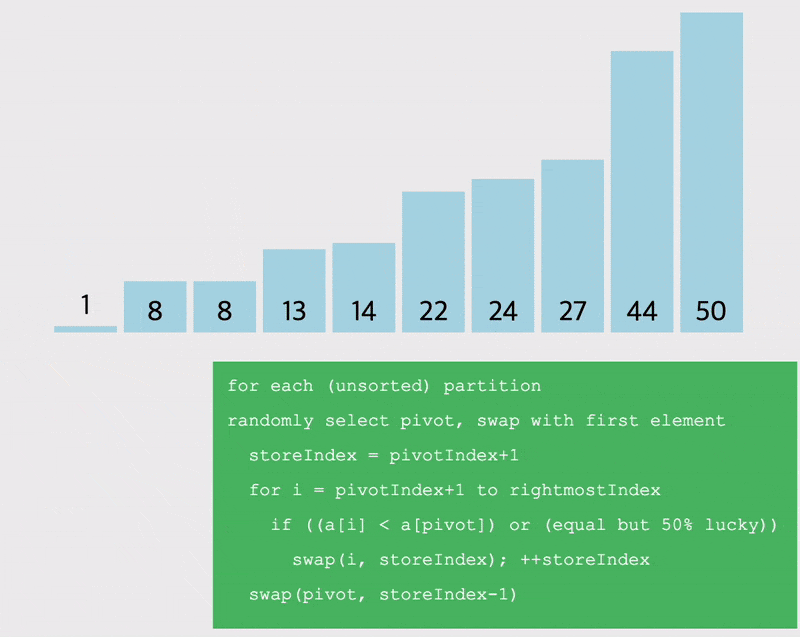
      # 퀵정렬 파티셔닝

      선정한 pivot을 기준으로 작은 값을 왼쪽, 큰 값을 오른쪽으로 이동시키는 방법을 생각해보자.

      퀵소트의 재귀적인 그림

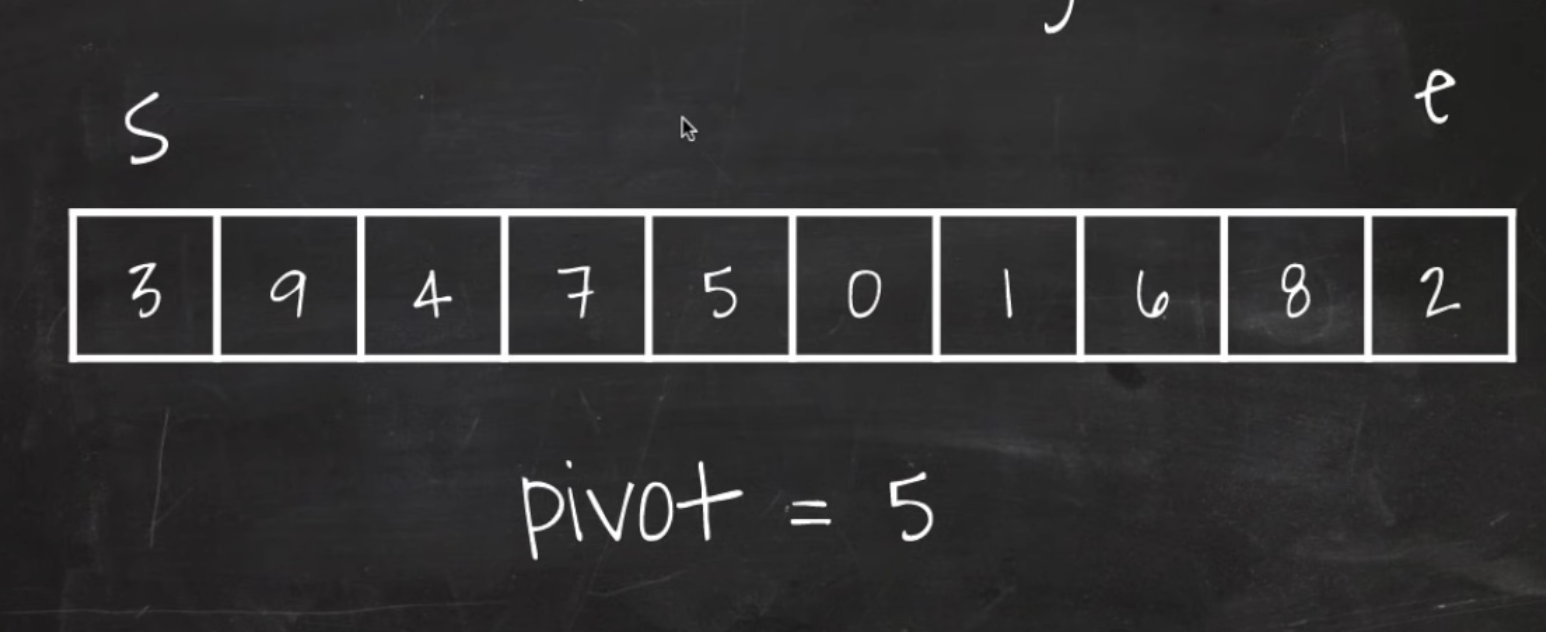
      1. start 인덱스는 pivot보다 작은 값을 무시하면서 +1씩
        • pivot보다 큰거 만나면 일단 대기
      2. end 인덱스는 pivot보다 큰 값을 무시하면서 -1씩
        • pivot보다 작은거 만나면 일단 대기
      3. start와 end를 서로 swap
      4. 그리고 다시 1,2,3 반복
      5. start와 end가 정한 범위를 넘어서면 루프 종료

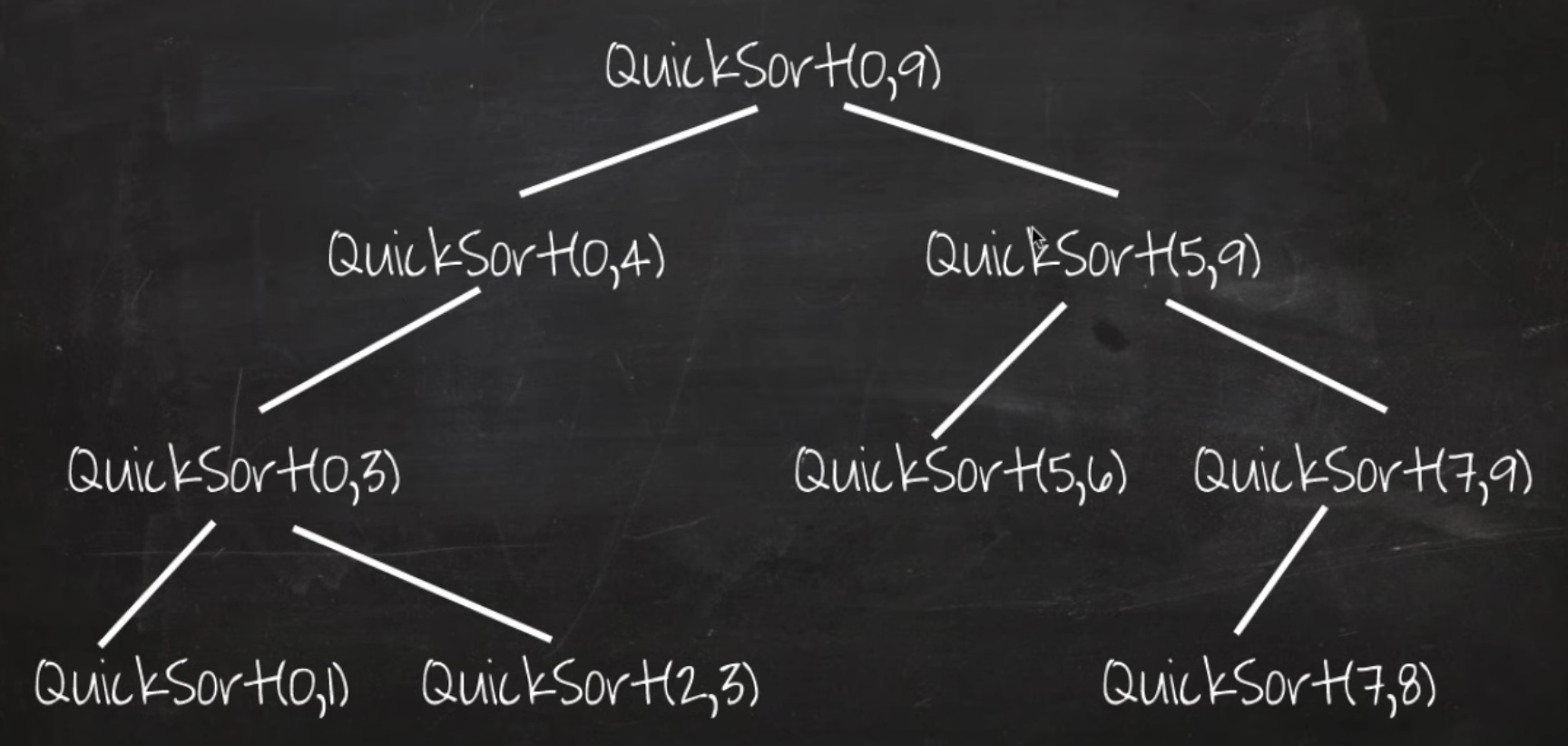
      • 이렇게 pivot을 기준으로 작은 값, 큰 값으로 파티셔닝을 나눔

      # 퀵정렬 구현


       1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57

      import java.util.Arrays;  
  
public class QuickSort {  
    private static void quickSort(int[] arr) {  
        quickSort(arr, 0, arr.length - 1);  
    }  
  
    // 파티션을 나눌 범위를 start, end 를 파라미터로 받음  
    private static void quickSort(int[] arr, int start, int end) {  
        // 해당 배열 방의 start ~ end 영역 안에서 파티션을 나누고  
        // 나눈 파티션의 오른쪽 방 첫번째 값을 part2가 받아옴  
        int part2 = partition(arr, start, end);  
        
        // 만약 오른쪽 파티션 part2가 시작점 start 의 바로 오른쪽에서 시작한다면  
        // 왼쪽 파티션의 데이터가 1개인거니까 그쪽은 정렬할 필요가 없음  
        // 그래서 오른쪽 파티션과 시작점이 1개 이상 차이가 날 때만 재귀호출 실행  
        if (start < part2 - 1) {  
            // 왼쪽 파티션이니까 시작점 ~ 오른쪽 파티션의 시작점 바로 이전  
            quickSort(arr, start, part2 - 1);  
        }  
  
        // 오른쪽 파티션의 배열 방이 1개 이상일 때만 재귀호출 해야함  
        // 오른쪽 파티션의 시작점인 part2가 end 보다 작을때만  
        if (part2 < end) {  
            quickSort(arr, part2, end);  
        }  
    }  
  
    private static int partition(int[] arr, int start, int end) {  
        int pivot = arr[(start + end) / 2];  
        while (start <= end) {  
            // start 인덱스의 값이 pivot 보다 작으면 무시하고 1 증가, 크면 일단 대기  
            while (arr[start] < pivot) start++;  
            // end 인덱스의 값이 pivot 보다 크면 무시하고 1 감소, 작으면 일단 대기  
            while (arr[end] > pivot) end--;  
            if (start <= end) {  
                swap(arr, start, end);  
                start++;  
                end--;  
            }  
        }  
        return start;  
    }  
  
    private static void swap(int[] arr, int start, int end) {  
        int temp = arr[start];  
        arr[start] = arr[end];  
        arr[end] = temp;  
    }  
  
    public static void main(String[] args) {  
        int[] arr = {2, 13, 4, 11, 9, 8, 1, 1, 10, 5};  
        System.out.println("Before Sorting : " + Arrays.toString(arr));  
        quickSort(arr);  
        System.out.println("After Sorting : " + Arrays.toString(arr));  
    }  
}

      # 참고

      Comment