삽입 정렬
Last updated -
2023년 04월 26일
Edit Source
# 삽입정렬 개념
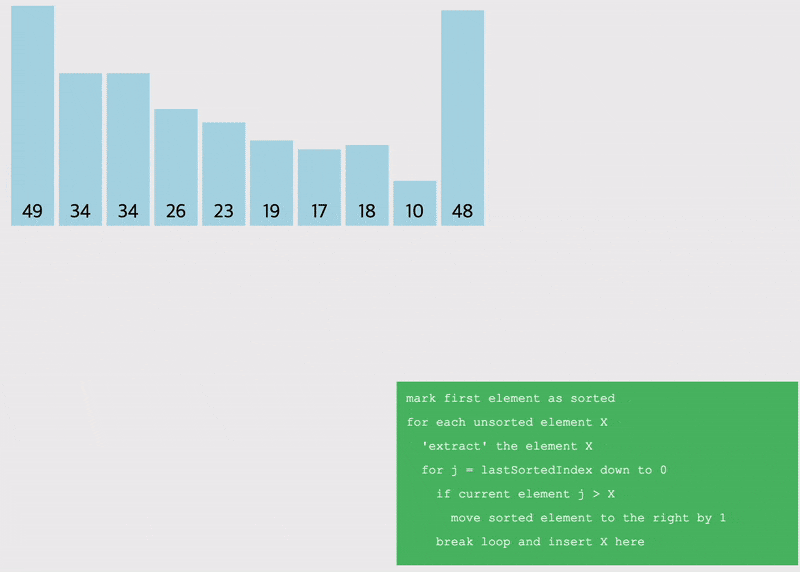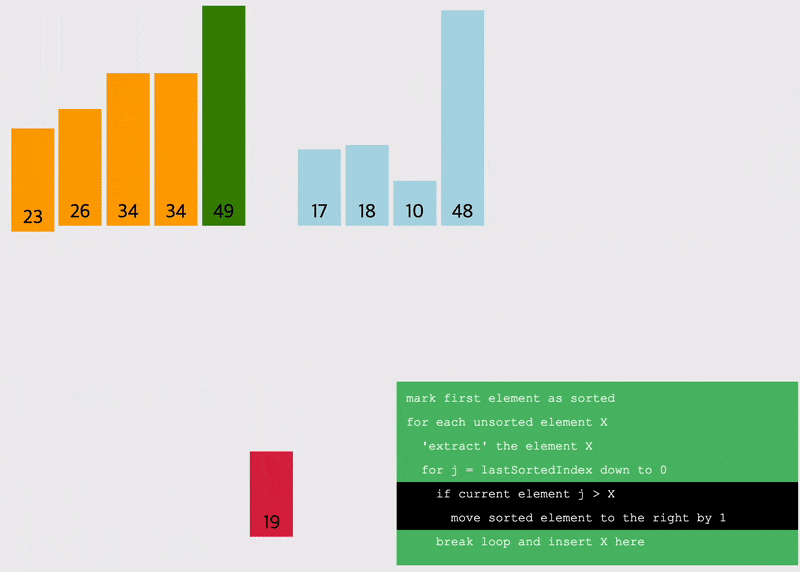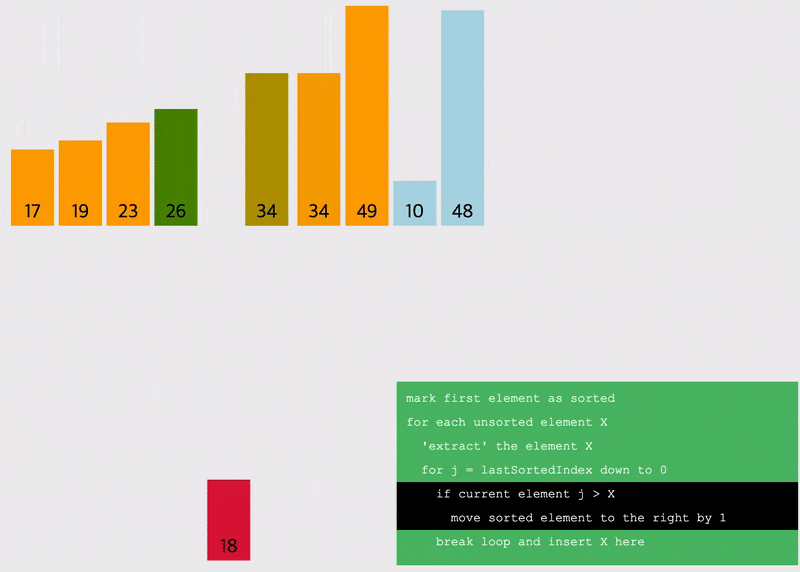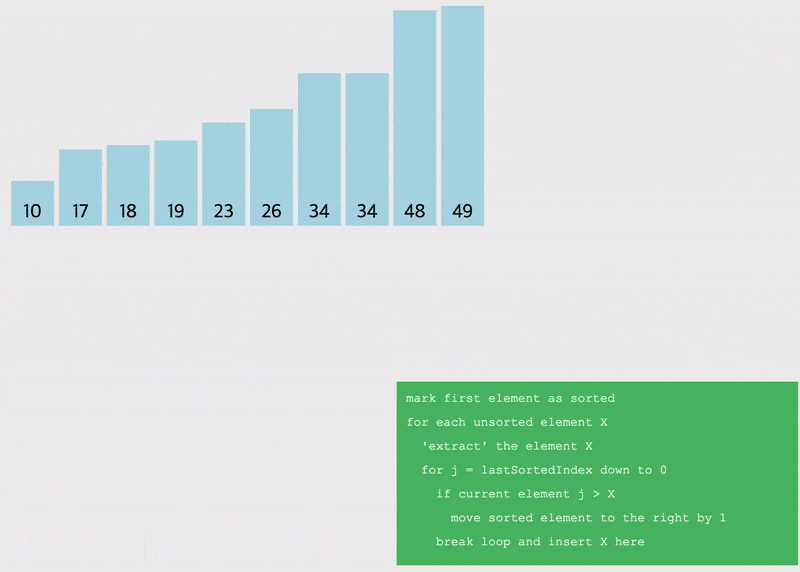
삽입정렬 (Insertion Sort) : 새로운 원소를 이전까지 정렬된 원소 사이에 올바르게 삽입시키는 알고리즘
- 0번째 인덱스는 앞에 숫자가 없어서 정렬의 시작은 1번째 인덱스임
- 1번째 인덱스부터 시작해서 앞의 원소들과 비교하며 삽입할 위치를 지정하고, 원소를 한칸씩 뒤로 다 땡기고 지정된 자리에 삽입하는 알고리즘
- 들어갈 위치가 있는 것으로 보아 선택정렬과 유사해보이지만, 더 효율적임
- 백준 줄세우기 문제가 삽입정렬임
- 시간복잡도 : $O(n^2)$
- 최선 : $O(n)$ (이미 정렬된 경우 + 최적화), 평균 : $O(n^2)$, 최악 : $O(n^2)$
- 외부 루프를 n-1번 도는 동안, 각 자리에 와야하는 값을 구하기 위해 n-1, n-2, … , 1번 비교
- $T(n) = (n-1) + (n-2) + … + 1 = (n-1) * \frac{n}{2}$
- 공간복잡도 : $O(1)$
- 교환(swap)을 통해 정렬이 수행되므로, 추가적인 배열 공간 필요없음
- 만약, 새로운 배열을 만들어서 거기 삽입하면, 그때는 공간복잡도 $O(n)$
- 안정성&제자리성 : 안정 정렬(Stable-sort), 제자리 정렬(In-place sort)
- 비교대상의 원소가 새로운 원소보다 클 때만 한자리 뒤로 이동시키니까 당연히 처음 순서가 유지되니까 → 안정
- 기존 배열 이외의 추가적인 메모리를 거의 사용하지 않고 배열 안에서 교환 → 제자리
# 삽입정렬 - 단순 반복
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| import java.util.Arrays;
public class Insertion {
private static void insertionSort(int[] arr) {
// 0번 인덱스는 앞에 숫자가 없으니까 1번 인덱스부터 시작
for (int i = 1; i < arr.length; i++) {
// 뒤에서부터 동작하는 이유는, 앞에서부터 값을 땡기면
// 그 값만 뒤로 복사돼서 그럼
for (int j = i - 1; j >= 0; j--) {
if (arr[j] > arr[j + 1])
swap(arr, j, j + 1);
}
}
}
private static void swap(int[] arr, int preIndex, int currentIndex) {
int temp = arr[preIndex];
arr[preIndex] = arr[currentIndex];
arr[currentIndex] = temp;
}
public static void main(String[] args) {
int[] arr = {3, 2, 1, 8, 4, 5, 7, 12, 3};
System.out.println("Before Sorting: " + Arrays.toString(arr));
insertionSort(arr);
System.out.println("After Sorting: " + Arrays.toString(arr));
}
}
|
# 삽입정렬 - 최적화 반복1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| import java.util.Arrays;
public class Insertion {
private static void insertionSort(int[] arr) {
for (int i = 1; i < arr.length; i++) {
int j = i - 1;
// while 안에다가 비교 작업을 넣어버렸음
while (j >= 0 && arr[j] > arr[j + 1]) {
swap(arr, j, j + 1);
j--;
}
}
}
private static void swap(int[] arr, int preIndex, int currentIndex) {
int temp = arr[preIndex];
arr[preIndex] = arr[currentIndex];
arr[currentIndex] = temp;
}
public static void main(String[] args) {
int[] arr = {3, 2, 1, 8, 4, 5, 7, 12, 3};
System.out.println("Before Sorting: " + Arrays.toString(arr));
insertionSort(arr);
System.out.println("After Sorting: " + Arrays.toString(arr));
}
}
|
- while문을 만들면서 안에다가 비교작업을 넣은 이유
- 삽입될 숫자보다 작은 숫자들은 이미 정렬 해놓았기 때문에 비교가 무의미해서
- 예를 들어,
[1, 2, 3, 5]가 있고 4를 추가하는 상황이면 3이 4보다 작다는 사실만 파악하면 됨. 이 이상의 대소 비교는 무의미
# 삽입정렬 - 최적화 반복2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| import java.util.Arrays;
public class Insertion {
private static void insertionSort(int[] arr) {
for (int i = 1; i < arr.length; i++) {
int current = arr[i];
int j = i - 1;
while (j >= 0 && arr[j] > current) {
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = current;
}
}
public static void main(String[] args) {
int[] arr = {3, 2, 1, 8, 4, 5, 7, 12, 3};
System.out.println("Before Sorting: " + Arrays.toString(arr));
insertionSort(arr);
System.out.println("After Sorting: " + Arrays.toString(arr));
}
}
|
- 사실 swap 작업도 필요 없음
- 앞의 값이 정렬 범위에 추가시킨 값보다 크면 앞의 값을 뒤로 밀고 제일 작은거 만나는 순간 그 뒤에 추가된 값을 꽂으면 됨
# 삽입정렬 - 재귀 구현
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| import java.util.Arrays;
public class Insertion {
private static void insertionSort(int[] arr) {
// 0번 인덱스는 앞에 숫자가 없으니까 1번 인덱스부터 시작
insertionSort(arr, 1);
}
private static void insertionSort(int[] arr, int start) {
// 배열의 마지막 방까지 재귀호출
if (start < arr.length) {
// 현재 숫자는 1부터 시작
int currentNum = arr[start];
// 삽입할 곳의 인덱스는 0부터 시작하니까 start - 1
int targetIndex = start - 1;
// 현재 숫자를 비교 대상들과 비교하여 삽입할 위치 찾기
// 뒤에서부터 동작하는 이유는, 앞에서부터 값을 땡기면 그 값만 뒤로 복사돼서 그럼
while (targetIndex >= 0 && currentNum < arr[targetIndex]) {
// 더 큰 값들을 오른쪽으로 이동
arr[targetIndex + 1] = arr[targetIndex];
targetIndex--;
}
// 현재 숫자를 삽입할 위치에 삽입
arr[targetIndex + 1] = currentNum;
// 다음 원소에 대해 재귀적으로 정렬 수행
insertionSort(arr, start + 1);
}
}
public static void main(String[] args) {
int[] arr = {3, 2, 1, 8, 4, 5, 7, 12, 3};
System.out.println("Before Sorting: " + Arrays.toString(arr));
insertionSort(arr);
System.out.println("After Sorting: " + Arrays.toString(arr));
}
}
|
